14. Ориентированные графы
Рассмотрим конечное Непустое множество 
мощности 
и множество 
мощности 
упорядоченных пар элементов множества 
.
Определение. Ориентированным графом 
называется пара множеств 
и 
.
Элементы множества 
называются Узлами Графа 
, элементы множества 
– его Дугами. Дуга 
, соединяющая два различных узла 
графа, обозначается упорядоченной парой 
, в которой 
– начало дуги, 
– конец дуги. На диаграмме ориентированного графа дуга изображается стрелкой, направление которой соответствует упорядоченности узлов.
Например, на рис. 23 приведена диаграмма ориентированного графа 
, имеющего четыре узла и четыре дуги.
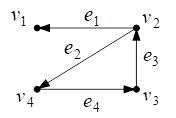
Рис. 23. Диаграмма ориентированного графа 
Множеством узлов графа является множество 
. Множеством дуг графа является множество 
с элементами 
, 
, 
, 
.
Понятия «подграф», «изоморфизм ориентированных графов», «смежность узлов», «инцидентность узлов и дуг» определяются так же, как соответствующие понятия неориентированных графов. В определениях этих понятий термин «вершина» заменяется термином «узел», термин «ребро» заменяется термином «дуга».
Путем в ориентированном графе называется открытый маршрут с различными дугами. Контуром Называется замкнутый маршрут с различными дугами.
Определение. Полустепенью исхода 
узла V называется число дуг, исходящих из этого узла. Полустепенью захода 
узла V называется число дуг, входящих в этот узел.
Определение. Степенью узла V Называется число 
.
Например, узлы ориентированного графа, диаграмма которого приведена на рис. 23, имеют следующие полустепени и степени:
, 
, 
; 
, 
, 
;
, 
, 
; 
, 
, 
.
Теорема 24. (Теорема Эйлера.) Сумма полустепеней исхода и полустепеней захода всех узлов ориентированного графа равна удвоенному числу его дуг:
.
Определение. Стоком Называется узел, для которого 
и 
.
Определение. Источником Называется узел, для которого 
и 
.
Определение. Изолированным Называется узел, для которого 
и 
.
Например, граф, диаграмма которого приведена на рис. 23, имеет сток 
. Источников и изолированных узлов у этого графа нет.
Определение. Матрицей смежности узлов 
ориентированного графа называется квадратная матрица порядка P, элементы которой определяются по правилу:
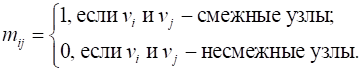
Индексы 
независимо друг от друга.
Например, матрицей смежности узлов графа, представленного на рис. 23, является квадратная матрица четвертого порядка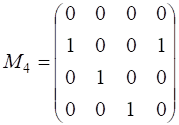 
.
Определение. Матрицей инцидентности 
ориентированного графа называется матрица размерности P на Q, элементы которой определяются по правилу:
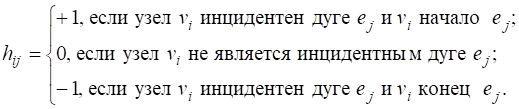
Например, матрицей инцидентности графа, представленного на рис. 23, является квадратная матрица четвёртого порядка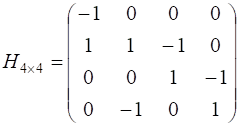 
.
Определение. Сильно связными называются два узла 
, для которых существуют пути из 
в 
и из 
в 
.
Например, у графа, диаграмма которого приведена на рис. 23, сильно связными являются узлы 
и 
, 
и 
, и 
.
Сильно связным называется граф, все узлы которого являются сильно связными.
Определение. Односторонне связными называются два узла 
, для которых существуют пути из 
в 
или из в .
Например, у графа, диаграмма которого приведена на рис. 23, односторонне связными являются узлы 
и 
, 
и 
, и 
, 
и , и , и .
Односторонне связным называется граф, все узлы которого являются односторонне связными.
Определение. Слабо связными Называются два узла 
, если они связны в соответствующем неориентированном графе.
Например, у граф, диаграмма которого приведена на рис. 23, слабо связными являются все пары узлов.
Слабо связным называется граф, все узлы которого являются слабо связными.
Теорема 25. Если два узла сильно связные, то они односторонне связные и слабо связные.
Определение. Сетью называется ориентированный граф 
с одним источником и одним стоком.
Задачи и упражнения
60. Из Череповца в Вологду выехали пятеро велосипедистов: Белов, Чернов, Краснов, Смирнов и Захаров. Чернов едет впереди Смирнова. Захаров едет впереди Белова, но позади Смирнова. Краснов – впереди Чернова. Определите, в каком порядке едут велосипедисты.
61. Для ориентированного графа с шестью узлами, заданного списком дуг 
,
1) постройте диаграмму;
2) составьте матрицы смежности и инцидентности;
3) найдите полустепени и степени всех узлов;
4) найдите число компонент связности, цикломатическое и хроматическое числа;
5) выполните правильную раскраску графа и найдите его классы одноцветности.
| < Предыдущая | Следующая > |
|---|
