13. Деревья

Рассмотрим граф , Имеющий P вершин и Q ребер.

Определение. Деревом называется связный граф без циклов.

Определение. Остовным деревом произвольного графа называется его Остовной подграф, являющийся Деревом.

Например, на рис. 20 представлено остовное дерево графа, диаграмма которого изображена на рис. 1.

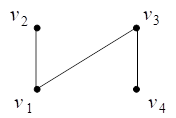
Рис. 20. Остовное дерево графа

Всякое дерево является двудольным графом.

Теорема 23.

1) Граф является деревом тогда и только тогда, когда .

2) Граф является деревом тогда и только тогда, когда Любые Две его вершины соединены единственной Простой цепью.

Пример. Волейбольная сетка имеет вид прямоугольника, состоящего из клеток. Какое наибольшее число веревочек можно перерезать так, чтобы сетка не распалась?

Решение. Рассмотрим граф, соответствующий клетчатому полю M на N, M = 50, N = 600. Число вершин графа равно
= . Число ребер графа равно
= . Сетка не распадётся до тех пор, пока соответствующий ей граф с вершинами и рёбрами будет связным. По условию задачи , а уменьшается. Пока связный граф содержит циклы, можно, не нарушая связности, удалять любое ребро цикла. Процесс продолжается до тех пор, пока не получится связный граф без циклов, то есть дерево. Дерево с вершинами имеет рёбер. Значит, можно удалить верёвочек. □

Теорема 24. Число Различных деревьев, которые можно построить на P занумерованных вершинах непустого графа, имеющего не менее двух вершин, равно .

Например, число различных деревьев, которые можно построить на четырёх занумерованных вершинах графа, представленного на рис. 1, равно 16.

Определение. Лесом называется несвязный граф без циклов.

Каждая компонента связности леса является деревом.

Например, на рис. 21 представлена диаграмма леса, имеющего две компоненты связности.

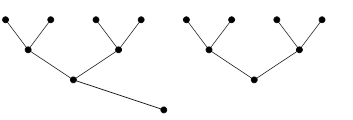
Рис. 21. Диаграмма леса

Определение. Весом ребра Графа называется действительное число, поставленное в соответствие этому ребру по специальному правилу.

Такой граф называется нагруженным. Вес графа равен сумме весов его ребер.

Например, на рис. 22 представлены нагруженный граф и его остовное дерево наименьшего веса.

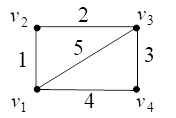
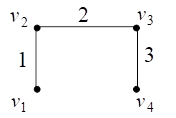
Рис. 22. Нагруженный граф и его остовное дерево наименьшего веса

Задачи и упражнения

54. Постройте диаграммы графов, заданных следующими матрицами смежности. Установите, являются ли эти графы деревьями.

1) 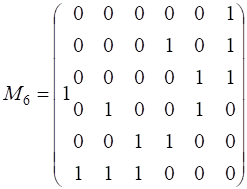; 2) .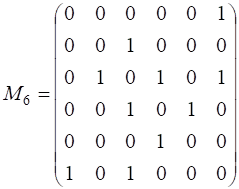

55. Дерево имеет три вершины степени 3 и четыре вершины степени 2. Остальные вершины дерева имеют степень 1. Сколько вершин дерева имеет степень 1?

56. Найдите все различные деревья графа .

57. Постройте диаграмму леса с семью вершинами и двумя компонентами связности. Найдите число его рёбер.

58. Найдите цикломатическое число дерева задачи 55.

59. В шахматном турнире по олимпийской системе участвуют 8 человек. Сколько всего встреч будет проведено?

< Предыдущая		Следующая >