1. Основные понятия теории функций комплексной переменной. Комплексные числа
Модуль комплексного числа ![]() Находится по формуле
Находится по формуле ![]() .
. ![]() - Действительная часть,
- Действительная часть, ![]() - Мнимая часть. Для нахождения Аргумента
- Мнимая часть. Для нахождения Аргумента ![]() (обозначение
(обозначение ![]() ) рекомендуется поставить в соответствие комплексному числу в декартовой системе координат на плоскости точку с координатами
) рекомендуется поставить в соответствие комплексному числу в декартовой системе координат на плоскости точку с координатами ![]() ,
, ![]() (см. рис. 1.1.1). Отсюда
(см. рис. 1.1.1). Отсюда
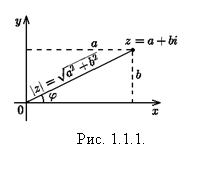

![]() - Тригонометрическая форма,
- Тригонометрическая форма, ![]() - Показательная форма и Формула извлечения целого корня:
- Показательная форма и Формула извлечения целого корня:
![]() . (1.1.1)
. (1.1.1)
Таким образом, корень ![]() - ой степени имеет
- ой степени имеет ![]() различных значений, которые получаются подстановкой
различных значений, которые получаются подстановкой ![]()
Пример 1.1.1. Найти все значения корня ![]() .
.
Решение. Находим модуль и аргумент комплексного числа ![]() :
: ![]() ;
; ![]() . По формуле (1.1.1)
. По формуле (1.1.1)
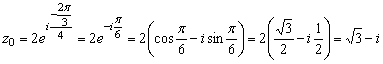 ;
;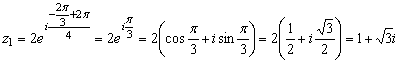 ;
; ;
;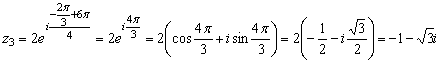 .
.
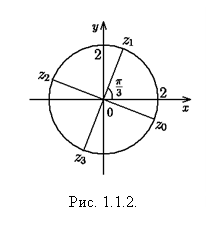 Ответ:
Ответ: ![]() ;
; ![]() ;
; ![]() ;
; ![]() (см. рис. 1.1.2).
(см. рис. 1.1.2).
 Сделаем важное замечание о том, что комплексные числа нельзя сравнивать. Действительно, два радиус-вектора, соответствующих изображению комплексных чисел на плоскости, можно только сравнить по длине, т. е. Комплексные числа сравнимы по модулю.
Сделаем важное замечание о том, что комплексные числа нельзя сравнивать. Действительно, два радиус-вектора, соответствующих изображению комплексных чисел на плоскости, можно только сравнить по длине, т. е. Комплексные числа сравнимы по модулю.
Пример 1.1.2. Изобразить на плоскости множество точек ![]() , для которых справедливо неравенство
, для которых справедливо неравенство ![]() .
.
Решение. Вычисляем модули: ![]() ,
, ![]() . Следовательно, комплексные числа
. Следовательно, комплексные числа ![]() удовлетворяют неравенству:
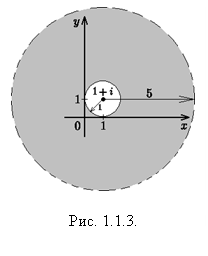
удовлетворяют неравенству: ![]() . Строим окружности с центром в точке
. Строим окружности с центром в точке ![]() и радиусами
и радиусами ![]() И
И ![]() , соответственно. Множество точек
, соответственно. Множество точек ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , изображается в виде кольца (см. рис. 1.1.3).
, изображается в виде кольца (см. рис. 1.1.3).
| Следующая > |
|---|