17. Существование производных всех порядков в области аналитичности функции комплексной переменной

Пусть F(z)Î C¥(). Тогда значения F(z) во всех внутренних точках области (ZÎg) можно выразить через значения F(z) на ¶g при помощи интеграла Коши .

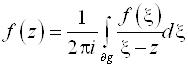Производная порядка N нашей подынтегральной функции по параметру Z равна 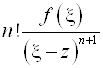=> она непрерывна везде внутри g => можно дифференцировать интеграл Коши произвольное число раз. Т. о. справедлива

Теорема 8.1. Пусть F(z)Î C¥(), тогда внутри g существуют производные произвольного порядка и верна формула

.

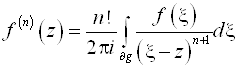Замечание. Существенное отличие комплексных функций от функций действительной переменной, для которых из существования первой производной, вообще говоря, не следует существование высших производных. Например, функция y(x)=x|x| непрерывна на всей числовой прямой; ее производная y'(x)=2|x| также непрерывна на всей числовой прямой, однако, y"(0) не существует!

< Предыдущая		Следующая >