5.3. Решение задач
Пример 1. Производится три независимых опыта, в каждом из которых событие A появляется с вероятностью 0,4. Рассматривается случайная величина X – число появлений события A в трех опытах. Построить ряд и многоугольник распределения, функцию распределения случайной величины X. Найти: 1) вероятность событий: A={X<2}; B={![]() }; C={
}; C={![]() }; 2) математическое ожидание
}; 2) математическое ожидание ![]() , дисперсию
, дисперсию ![]() , среднее квадратическое отклонение
, среднее квадратическое отклонение ![]() случайной величины X.
случайной величины X.
Решение. Случайная величина X может принимать значения ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Соответствующие им вероятности
. Соответствующие им вероятности ![]() найдем, воспользовавшись формулой Бернулли. При n=3,
найдем, воспользовавшись формулой Бернулли. При n=3, ![]() ;
; ![]() имеем:
имеем: ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Отсюда ряд распределения случайной величины X имеет вид:
![]()
(Контроль: ![]() ).
).
Многоугольник распределения случайной величины X представлен на рис.6.
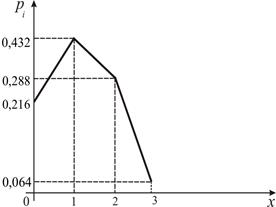
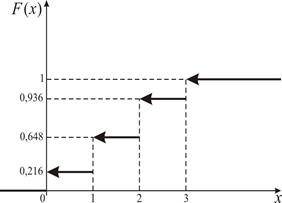
Рис. 6 Рис. 7
Найдем функцию распределения F(x). По определению функции распределения имеем: если ![]() , то
, то ![]() ;
;
Если ![]() , то
, то ![]() ;
;
Если ![]() , то
, то ![]() ;
;
Если ![]() , то
, то ![]() ;
;
Если ![]() , то
, то ![]()
![]() .
.
Итак, 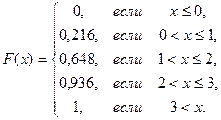
График функции F(x) изображен на рис. 7.
1) Сначала вычислим искомые вероятности непосредственно:
![]() ;
;
![]() ;
;
![]() .
.
Эти же вероятности найдем, воспользовавшись формулами:
![]() и
и ![]() . Тогда
. Тогда ![]() ;
;
![]() ;
;
![]()
2) Найдем математическое ожидание случайной величины X. Используя формулу (3), получим ![]() . Вычислим дисперсию. По формуле (6) имеем:
. Вычислим дисперсию. По формуле (6) имеем:
![]() =0,72. Тогда среднее квадратическое отклонение
=0,72. Тогда среднее квадратическое отклонение ![]() .
.
Пример 2. Дан ряд распределения дискретной случайной величины X:
![]()
Найти моду.
Решение. Так как дискретная случайная величина X принимает значение ![]() с наибольшей вероятностью
с наибольшей вероятностью ![]() по сравнению с двумя соседними значениями, то мода случайной величины X равна 20, т. е.
по сравнению с двумя соседними значениями, то мода случайной величины X равна 20, т. е. ![]() .
.
Пример 3. Дана функция
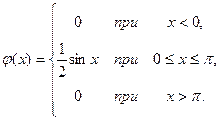
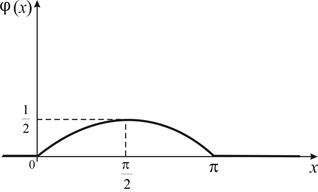
Рис. 8
Показать, что ![]() может служить плотностью вероятности некоторой случайной величины X.. Найти математическое ожидание и дисперсию случайной величины X.
может служить плотностью вероятности некоторой случайной величины X.. Найти математическое ожидание и дисперсию случайной величины X.
Решение. Используя свойство нормированности плотности распределения, найдем, что
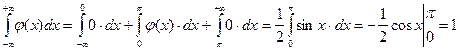 ,
,
Кроме того, ![]() . Следовательно,
. Следовательно, ![]() может служить плотностью вероятности некоторой случайной величины. Так как прямая
может служить плотностью вероятности некоторой случайной величины. Так как прямая ![]() является осью симметрии соответствующей дуги кривой
является осью симметрии соответствующей дуги кривой ![]() (см. рис.8), то математическое ожидание случайной величины X равно
(см. рис.8), то математическое ожидание случайной величины X равно ![]() , т. е.
, т. е. ![]() . Найдем дисперсию, воспользовавшись формулой (8). Двукратным интегрированием по частям получим:
. Найдем дисперсию, воспользовавшись формулой (8). Двукратным интегрированием по частям получим:
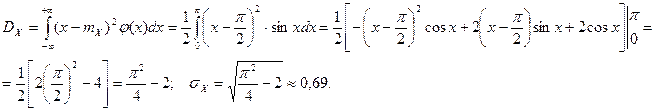
Пример 4. Дана плотность вероятности случайной величины X;
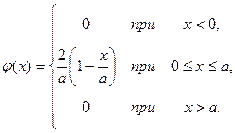
Найти функцию распределения F(X), вероятность попадания случайной величины X в промежуток ![]() , числовые характеристики величины X:
, числовые характеристики величины X: ![]() .
.
Решение. Найдем функцию распределения случайной величины X, для этого воспользуется соотношением (1).
Если x < 0, то ![]() .
.
Если ![]() , то
, то 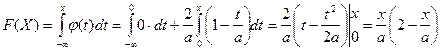 .
.
Если x > a, то 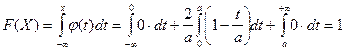 .
.
Итак, 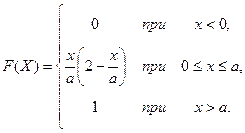
По формуле (*) имеем ![]() .
.
Найдем математическое ожидание случайной величины X. Согласно формуле (5)
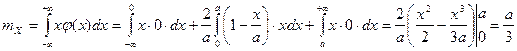 .
.
Теперь отыщем дисперсию. По формуле (8)
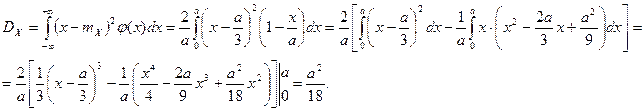 Отсюда среднее квадратическое отклонение
Отсюда среднее квадратическое отклонение ![]() .
.
Пример 5. Найти моду, медиану, математическое ожидание и функцию распределения случайной величины X с плотностью вероятности
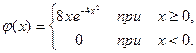
Решение. Найдем точку максимума функции ![]() :
: ![]() ; отсюда
; отсюда![]() при
при ![]() . Точка
. Точка ![]() является точкой максимума функции
является точкой максимума функции ![]() , так как
, так как ![]() , если
, если ![]() и
и ![]() , если
, если ![]() . Следовательно, мода
. Следовательно, мода ![]() .
.
Медиану ![]() определим из условия (9):
определим из условия (9): ![]() (или
(или ![]() ).
).
В данном случае по формуле (2): 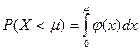 , т. е.
, т. е. 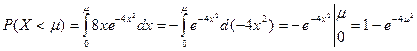 .
.
Таким образом, приходим к уравнению: ![]() или
или ![]() . Отсюда,
. Отсюда, ![]() .
.
Воспользовавшись формулой (5), вычислим математическое ожидание случайной величины X:
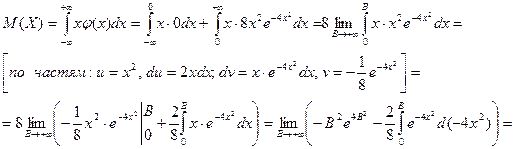
![]()
Найдем функцию распределения случайной величины X.
Прежде всего заметим, что если x < 0, то ![]()
Если же ![]() то
то 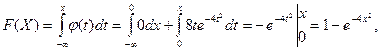 т. е.
т. е. ![]() .
.
| < Предыдущая | Следующая > |
|---|