5.2. Мода и медиана

Кроме математического ожидания и дисперсии в теории вероятностей применяется еще ряд числовых характеристик, в частности, мода и медиана случайной величины.

Модой Дискретной случайной величины X называется ее наиболее вероятное значение.

Модой непрерывной случайной величины X называется такое ее значение , при котором плотность распределения Имеет максимум, т. е. .

На рис. 3 и 4 показана мода для дискретной и непрерывной случайной величины.

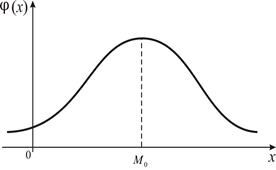
Рис. 3 Рис. 4

Если многоугольник распределения (кривая распределения) имеет два или несколько максимумов, то распределение называется Двухмодальным или многомодальным.

Иногда встречаются распределения, которые имеют минимум, но не имеют максимум. Такие распределения называются Антимодальными.

Медианой непрерывной случайной величины X (обозначение:) называется такое ее значение , для которого одинаково вероятно, окажется ли случайная величина Меньше или больше, т. е.

. (9)

Геометрически вертикальная прямая , Проходящая через точку с абсциссой, равной , делит площадь фигуры под кривой распределения на две равные части (рис. 5). Каждая из этих площадей равна , т. к. площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке равна , т. е. .

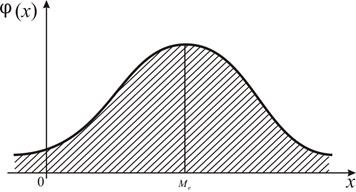
Рис. 5

Для дискретной случайной величины медиана обычно не определяется.

< Предыдущая		Следующая >