4. Функция распределения и плотность вероятности непрерывной случайной величины

С помощью функции распределения можно дать более строгое определение непрерывной случайной величины.

Случайная величина X называется Непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

В отличие от дискретных случайных величин вероятность отдельного значения для непрерывной случайной величины равна нулю: . Поэтому для непрерывной случайной величины X имеем

. (*)

Для Непрерывных случайных величин кроме функции распределения существует еще один удобный способ задания Закона распределения – плотность вероятности.

Пусть функция распределения данной непрерывной случайной величины X непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек.

Плотностью распределения непрерывной случайной величины X (или Плотностью вероятности, или просто Плотностью) называется функция .

Функцию называют также Дифференциальной функцией распределения.

Плотность распределения любой непрерывной случайной величины неотрицательна, т. е. ; обладает свойством нормированности:

; .

График функции называется Кривой распределения.

Функция распределения F(x) выражается через плотность распределения формулой

(1)

Вероятность попадания непрерывной случайной величины в промежуток определяется равенством:

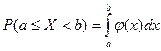. (2)

< Предыдущая		Следующая >