12. Однородная система линейных уравнений и ее решения

Определение 22

Система линейных уравнений

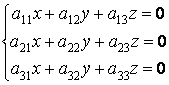
У которой столбец свободных членов - нулевой, называется однородной.

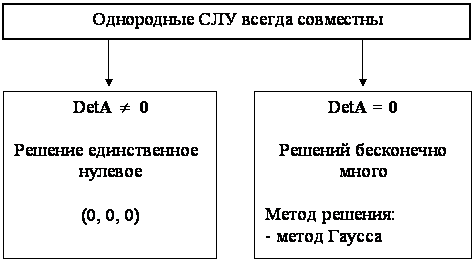
Однородная СЛУ (ОСЛУ) всегда совместна, так как нулевое решение (0,0,0) ей всегда удовлетворяет.

Поэтому, если однородная СЛУ имеет единственное решение, тогда оно - нулевое, так как для данного вида систем нулевое решение всегда имеет место.

Однородная СЛУ имеет ненулевые решения, если решений бесконечно много.

Утверждение 9. (Критерий существования ненулевых решений ОСЛУ).

Для того, чтобы однородная СЛУ имела ненулевые решения, необходимо и достаточно, чтобы определитель системы был равен нулю.

 

 

 

 

 

 

 

 

 

 

 

 

Пример №31. Решить однородную СЛУ

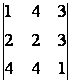= = 30

Определитель однородной системы отличен от нуля, следовательно решение единственное – нулевое.

Ответ: (0,0,0).

Пример №32. Решить однородную СЛУ

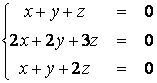
= = 0

Определитель однородной системы равен нулю, следовательно - решений бесконечно много.

Общее решение ищем с помощью метода Гаусса

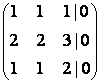
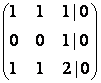
Далее записываем систему, соответствующую полученной ступенчатой матрице, и являющуюся эквивалентной исходной.

=> => ,

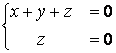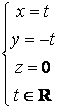
< Предыдущая		Следующая >