09. Обратная матрица

Определение 21

Матрица называется обратной матрице , если

= =

Где = - единичная матрица.

Единичная матрица в матричной алгебре играет роль единицы:

= = , где – квадратная матрица.

Вычисление обратной матрицы

=

Где = 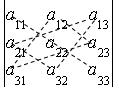- определитель матрицы

- алгебраические дополнения элементов

Пример №29. Вычислить матрицу , обратную матрице

=

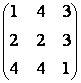
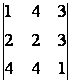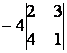
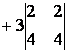= = = 30;

== ; == ;

== ; == ;

== ; == ;

== ;

== ; == ;

====

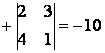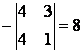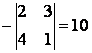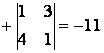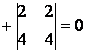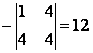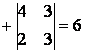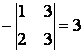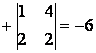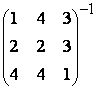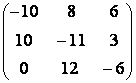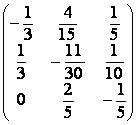
Проверка = =

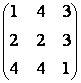
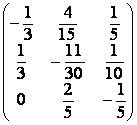Утверждение 8. (Критерий существования обратной матрицы)

Для существования необходимо и достаточно, чтобы det.

< Предыдущая		Следующая >