01. Введение в терминологию теории систем линейных уравнений

Определение 1

Системой линейных уравнений (СЛУ) с тремя неизвестными называется выражение вида:

Где

,, - неизвестные переменные,

,(=1,2,3, =1,2,3) - постоянные коэффициенты при неизвестных ,,

,(=1,2,3) - свободные члены уравнений,

- индекс, указывающий номер уравнения,

- индекс, указывающий номер неизвестной в уравнении.

Определение 2

Решением СЛУ c тремя неизвестными называется упорядоченная тройка чисел (,,), удовлетворяющая всем уравнениям системы.

Т. е., упорядоченный набор чисел (,,) называется решением СЛУ, если он обращает в тождества все уравнения системы при подстановке в них =, =, =.

Пример №1. Для СЛУ

Тройка чисел (1,2,3) является решением.

Определение 3

СЛУ называется совместной, если она имеет хотя бы одно решение;

В противном случае, если решений нет, СЛУ называется несовместной.

В примере №1 показана совместная система.

СЛУ может иметь бесконечно много решений.

Пример №2. Легко проверить что, СЛУ

Имеет бесконечно много решений.

Действительно, бесконечно много упорядоченных троек чисел удовлетворяет ей, например: (0,3,3), (1,2,3), (2,1,3), и т. д.

Эти решения получены из общей записи решения СЛУ:

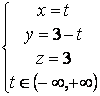
Решение (0,3,3) получается из общего решения, если параметр = 0.

Решение (1,2,3) - при = 1.

Решение (2,1,3) - при = 2, и т. д.

Определение 4

Совместная СЛУ называется определенной, если она имеет единственное решение; и - неопределенной, если решений бесконечно много.

В примере №2 показана совместная неопределенная СЛУ.

Пример №3. Легко проверить, что для СЛУ

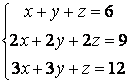
Не существует ни одного упорядоченного набора чисел, который удовлетворял бы всем уравнениям системы одновременно.

Действительно, умножая левую и правую части второго уравнения на , получим противоречивую систему

В данной системе первые два уравнения не могут одновременно выполняться ни при каких значениях переменных , , .

В примерах №1 и №2 показаны совместные системы.

В примере №3 – система несовместна.

Определение 5

Решить СЛУ – это значит найти все ее решения, или доказать, что система решений не имеет.

Следующая >