22. Квадратичная функция, ее график, квадратное уравнение
§ 22. Квадратичная функция 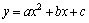 , ее график,
, ее график,
квадратное уравнение
Частный случай этой функции ![]() дает каноническое уравнение параболы, рис.1.11 (в, г) см. § 1.7.
дает каноническое уравнение параболы, рис.1.11 (в, г) см. § 1.7.
В общем случае это уравнение параболы с осью, параллельной оси ОY и произвольной вершиной.
Квадратное уравнение ![]() имеет два корня:
имеет два корня: ![]() ,
, ![]() , где дискриминант уравнения
, где дискриминант уравнения ![]() . В этом случае квадратичную функцию можно представить в виде:
. В этом случае квадратичную функцию можно представить в виде: ![]()
![]() . При
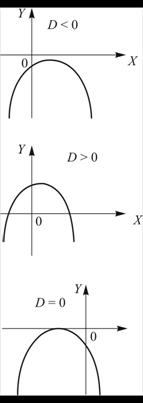
. При ![]() ветви параболы направлены вверх, а при
ветви параболы направлены вверх, а при ![]() – вниз.
– вниз.
Если ![]() , то
, то ![]() , т. е. оба корня совпадают – парабола касается оси ОХ.
, т. е. оба корня совпадают – парабола касается оси ОХ.
В этом случае говорят, что ![]() является корнем квадратности два. В случае
является корнем квадратности два. В случае ![]() , корнями квадратного уравнения являются два комплексных числа. График квадратичной функции не пересекает ось OX.
, корнями квадратного уравнения являются два комплексных числа. График квадратичной функции не пересекает ось OX.
Комплексные числа вводятся с помощью символа ![]() , этот символ называют мнимой единицей. Комплексное число имеет вид:
, этот символ называют мнимой единицей. Комплексное число имеет вид: ![]() , где A и B – вещественные числа. Число A называют вещественной частью Z и обозначают:
, где A и B – вещественные числа. Число A называют вещественной частью Z и обозначают: ![]() , а число B – мнимой частью числа Z:
, а число B – мнимой частью числа Z: ![]() . Алгебраические действия над комплексными числами производят по обычным правилам алгебры, при этом
. Алгебраические действия над комплексными числами производят по обычным правилам алгебры, при этом ![]() ;
; ![]() ;
; ![]() . Например,
. Например, ![]()
![]() . Произвольному числу Z Ставится в соответствие сопряженное число
. Произвольному числу Z Ставится в соответствие сопряженное число ![]() , при этом
, при этом ![]() – это вещественное число.
– это вещественное число.
При ![]() корни квадратного уравнения имеют вид:
корни квадратного уравнения имеют вид: ![]() ,
, ![]() , т. е. являются взаимно сопряженными комплексными числами. Таким образом, квадратное уравнение всегда имеет два корня: два разных вещественных числа, либо одно вещественное число кратности два, либо два комплексно–сопряженных числа.
, т. е. являются взаимно сопряженными комплексными числами. Таким образом, квадратное уравнение всегда имеет два корня: два разных вещественных числа, либо одно вещественное число кратности два, либо два комплексно–сопряженных числа.
График функции ![]() приведен на рис. 1.2.
приведен на рис. 1.2.
|
|
|
|
|
|
|
Рисунок 1.2 |
| < Предыдущая | Следующая > |
|---|