10. Производная функции, ее геометрический. И физический смысл
Введение бесконечно малых и больших величин связано с процессом их изменения. Изменения, как правило, характеризуют разностью между конечным (или соседним) и начальным значением. В математике, как и в физике, такую разность называют приращением. Приращение может быть положительным, когда соседнее (последующее) значение больше начального, и отрицательным. Мы постоянно встречаемся с характеристиками функции в точке: предел, непрерывность, значение самой функции. Определим понятие производной (от) функции в точке.
На рис.6 приведен график некоторой непрерывной функции ![]() .
.
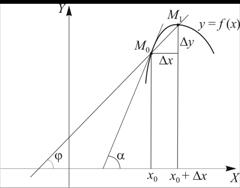
Рисунок 6 – Касательная прямая в М0 к графику функции есть предельное положение секущей М0 М1 При ![]()
Геометрический смысл производной: ![]() .
.
Точке М0 отвечает пара чисел ![]() , где
, где ![]() . Изменим значение Х0, т. е. дадим ему приращение DХ и, таким образом, от точки Х0 на оси абсцисс перейдем в точку Х0 + DХ. Вследствие этого точка М0 на графике передвинется в точку М1. Изменение функции в результате этого перехода обозначим
. Изменим значение Х0, т. е. дадим ему приращение DХ и, таким образом, от точки Х0 на оси абсцисс перейдем в точку Х0 + DХ. Вследствие этого точка М0 на графике передвинется в точку М1. Изменение функции в результате этого перехода обозначим ![]() . Отношение
. Отношение ![]() показывает, как быстро изменяется функция с изменением Х. Предел этого отношения при
показывает, как быстро изменяется функция с изменением Х. Предел этого отношения при ![]() называется производной функции в точке Х0.
называется производной функции в точке Х0.
Def: Производной функции У по аргументу Х называется предел отношения приращения функции DУ к приращению аргумента DХ, вычисленный в процессе, когда приращение аргумента стремится к нулю.
На рис.6 прямая линия, соединяющая две соседние точки М0 и М1, будет секущей для графика. Она наклонена к оси ОХ под углом j, и ![]() .
.
Если DХ устремим к нулю, то точка М1 начнет передвигаться по графику к точке М0, а секущая М0М1 поворачиваться относительно точки М0.
В пределе, при слиянии движущейся точки М1 с неподвижной М0 секущая займет положение касательной. Угол наклона касательной к оси ОХ равен ![]() . Таким образом,
. Таким образом, ![]()
Отсюда следует геометрический смысл производной:
Производная функции ![]() в точке
в точке ![]() равна тангенсу угла наклона касательной к графику функции в этой точке:
равна тангенсу угла наклона касательной к графику функции в этой точке: ![]() .
.
В начальной школе мы проходили уравнение прямой с угловым коэффициентом: ![]() . В старших классах мы обнаружили, что угловой коэффициент равняется тангенсу угла наклона прямой к оси ОХ. Сейчас мы отмечаем, что угловой коэффициент касательной
. В старших классах мы обнаружили, что угловой коэффициент равняется тангенсу угла наклона прямой к оси ОХ. Сейчас мы отмечаем, что угловой коэффициент касательной ![]() равен значению производной функции в точке касания:
равен значению производной функции в точке касания: ![]() . Это позволяет нам записать уравнение самой касательной:
. Это позволяет нам записать уравнение самой касательной: ![]() .
.
Кроме касательной в каждой точке графика часто рассматривают еще одну прямую, называемую нормалью.
Def: Прямая, проходящая через точку М0 перпендикулярно к касательной, называется нормалью к кривой в точке М0.
Уравнение нормали: ![]()
Для потребностей техники приходится рассматривать пространственные кривые, извивающиеся и закручивающиеся. Каждую точку такой кривой «сопровождает» совокупность трех единичных векторов, направленных один по касательной, второй по нормали, а третий вектор перпендикулярен к каждому из двух названных. Положение этих векторов определяют через производную от функции (или функций), описывающих кривую. И этот приём применения производных оказался исключительно эффективным при решении многих задач. Соответствующий раздел математики получил название дифференциальной геометрии.
Мы уже рассматривали функции, имеющие точки разрыва. В этих точках функция не имеет предела. Естественно ожидать, что предел отношения двух приращений ![]() и
и ![]() тоже не везде существует, т. е. не везде существует производная.
тоже не везде существует, т. е. не везде существует производная.
Def: Функция называется дифференцируемой в точке, если она имеет производную в этой точке. Функция называется дифференцируемой на интервале, если она имеет производную в каждой точке этого интервала.
Конечно, в точках разрыва, функция не может быть дифференцируема. А вот обратное утверждение неверно.
На рис.7 представлен график функции, непрерывной во всех точках, но не имеющей производных в точках М1, М2, М3.
В точке М1 функция не дифференцируема. К этой точке непрерывности примыкают два разных участка с разными касательными. В точке М2 также примыкают две разные ветви, но они имеют общую касательную, перпендикулярную оси ОХ. Следовательно, ![]() тоже не существует. Точка М3 разделяет вогнутый (слева) участок графика от выпуклого. В этой точке касательная тоже перпендикулярна к оси абсцисс:
тоже не существует. Точка М3 разделяет вогнутый (слева) участок графика от выпуклого. В этой точке касательная тоже перпендикулярна к оси абсцисс: ![]() .
.

Рисунок 7 – График непрерывной во всех точках функции.
В точках X1, X2, X3 функция не дифференцируема. В точке X1 примыкают две ветви графика с разными касательными; в точках X2 и X3 касательная к графику наклонена к оси ОХ
Под углом 90° (tg 90° – не существует)
Рассмотрим классический пример применения производной. Он связан с прямолинейным движением. Измерим время DT движения от одного дорожного столба до соседнего. Зная, с каким шагом DS устанавливаются столбы, находим среднюю скорость движения на этом конкретном участке ![]() . Переходя к пределу (уменьшая DT)
. Переходя к пределу (уменьшая DT)![]() Находим мгновенную скорость.
Находим мгновенную скорость.
| < Предыдущая | Следующая > |
|---|