2.2. Линейные действия над векторами и их свойства

Под линейными действиями над векторами понимаются следующие операции:

— сложение векторов;

— умножение вектора на число.

Определение 9. Сложение Двух векторов и осуществляется следующим образом:

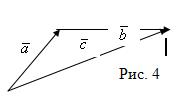
А) путем параллельного переноса начало вектора совмещается с концом вектора (см. рис. 4);

Б) строится третий вектор , начало которого совпадает с началом вектора , а конец — с концом вектора . Полученный вектор называется Суммой Векторов и , и обозначается .

Определение 10. При Умножении Вектора На число получается вектор, который обозначается и определяется следующим образом:

, где — модуль вектора , — модуль вектора .

Если , то направление вектора совпадает с направлением вектора .

Если , то направление вектора противоположно направлению .

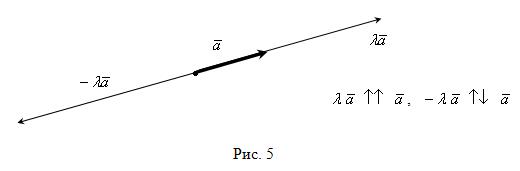
Пример 7. Вектор вытянут относительно в раз, если (см. рис. 5).

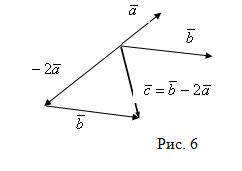
Пример 8. Построить вектор .

Решение:

Свойства линейных действий над векторами

1. = (коммутативность).

2. = (ассоциативность).

3. (дистрибутивность).

4. (дистрибутивность).

< Предыдущая		Следующая >