§ 02. Понятие функции
Пусть Х и Y – некоторые числовые множества и пусть указано правило, по которому каждому элементу Х множества Х поставлено в соответствие единственное значение У из множества Y. Это соответствие называется Функцией и обозначается ![]() . Переменная Х называется независимой или Аргументом, переменная У – зависимой или Функцией. Множество Х называется Областью определения Функции и обозначается D(F ). Множество Y (множество всех значений, которые принимает переменная У) называется Областью изменения (Областью значений) функции и обозначается E(F ).
. Переменная Х называется независимой или Аргументом, переменная У – зависимой или Функцией. Множество Х называется Областью определения Функции и обозначается D(F ). Множество Y (множество всех значений, которые принимает переменная У) называется Областью изменения (Областью значений) функции и обозначается E(F ).
Две функции называются равными, если они имеют одинаковые области определения и каждому значению аргумента они ставят в соответствие одно и тоже число.
Наиболее распространенный способ задания функции – Аналитический, то есть с помощью формулы. Например, функцию, ставящую в соответствие каждому неотрицательному числу х его квадратный корень, можно записать в виде ![]() или
или ![]() . Этот способ задания функции компактен, содержит полную информацию о свойствах функции и наиболее удобен при проведении расчетов. Если не сделано специальной оговорки, то за область определения функции берут все значения аргумента, для которых указанные в формуле действия выполнимы. Например, область определения функции
. Этот способ задания функции компактен, содержит полную информацию о свойствах функции и наиболее удобен при проведении расчетов. Если не сделано специальной оговорки, то за область определения функции берут все значения аргумента, для которых указанные в формуле действия выполнимы. Например, область определения функции ![]() все неотрицательные значения Х, то есть
все неотрицательные значения Х, то есть ![]() , а для функции
, а для функции ![]() – область определения все действительные значения Х, кроме
– область определения все действительные значения Х, кроме ![]() , то есть D(G) = ¡\{2}.
, то есть D(G) = ¡\{2}.
Иногда для разных значений Х функция задается разными формулами. В этом случае используют обозначение: 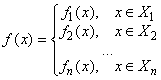 , причем
, причем ![]() . График такой функции состоит из N частей.
. График такой функции состоит из N частей.
На практике часто используют Табличный способ задания функции. При этом способе задания функции приводится таблица, в которой для имеющихся значений аргумента указываются соответствующие значения функции. Табличный способ важен потому, что он является основным при описании реальных зависимостей, возникающих при проведении различных экспериментов. С математической точки зрения табличное задание функции неполно, так как оно позволяет найти значение функции только для тех значений аргумента, которые заданы в таблице. Однако оно позволяет высказать предположение об аналитическом представлении функции, и, применяя различные методы приближенных вычислений, найти это представление.
Рассмотрим декартову систему координат на плоскости. Множество точек плоскости, координаты которых удовлетворяют условию ![]() , называется Графиком функции Y = F (X). Графическое представление функции удобно для непосредственного восприятия ее особенностей, описания свойств. Однако графический способ неудобен при выполнении расчетов.
, называется Графиком функции Y = F (X). Графическое представление функции удобно для непосредственного восприятия ее особенностей, описания свойств. Однако графический способ неудобен при выполнении расчетов.
 Функции можно также задавать Словесно. Например, функция Дирихле задается таким описанием: значение функции равно 1, если X рационально, и 0, если X иррационально.
Функции можно также задавать Словесно. Например, функция Дирихле задается таким описанием: значение функции равно 1, если X рационально, и 0, если X иррационально.
Примеры функций:
|
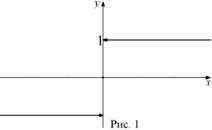
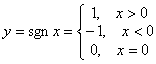 .
.
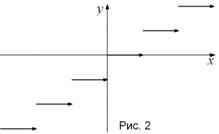 2. Функция
2. Функция ![]() каждому числу
каждому числу ![]() , где N Î ¢, ставит в соответствие число N (рис. 2). Эта функция называется Целой частью числа Х и обозначается
, где N Î ¢, ставит в соответствие число N (рис. 2). Эта функция называется Целой частью числа Х и обозначается ![]() .
.
![]()
![]()
![]() 3. Функция
3. Функция ![]() каждому числу
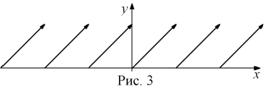
каждому числу ![]() , где N Î ¢, ставит в соответствие число
, где N Î ¢, ставит в соответствие число ![]() (рис. 3). Эта функция называется Дробной частью числа Х и обозначается
(рис. 3). Эта функция называется Дробной частью числа Х и обозначается ![]() .
.
| < Предыдущая | Следующая > |
|---|