16. Тест по теме «Применение регрессионных моделей»
1. Сравнить силу влияния факторов на исследуемый показатель можно, используя:
А) коэффициенты регрессии в натуральном масштабе из многофакторной модели регрессии;
Б) частные коэффициенты эластичности;
В) стандартизованные коэффициенты регрессии из многофакторного анализа.
2. Два фактора должны быть признаны коллинеарными, если
А) величина коэффициента корреляции между ними больше 0,7;
Б) величина коэффициента корреляции между ними меньше 0,7;
В) коэффициент корреляции между ними по модулю больше 0,7.
3. Совокупность наблюдений можно считать однородной по показателю хj, если коэффициент вариации (в %)
А) равен 33;
Б) меньше 33;
В) больше 33;
4. Задачами корреляционно-регрессионного анализа являются:
А) изучить оценки неизвестных параметров уравнения;
Б) оценить адекватность модели;
В) качественно предсказать результат в будущем;
Г) определить тесноту связи между показателями.
5. Значения линейного коэффициента корреляции могут находиться в границах:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]()
6. Множественный коэффициент корреляции характеризует тесноту связи между
А) несколькими зависимыми переменными и одной независимой переменной;
Б) несколькими зависимыми и несколькими независимыми переменными;
В) одной зависимой переменной и несколькими независимыми переменными;
Г) одной зависимой и одной независимой переменными.
7. Стандартизованный коэффициент регрессии рассчитывают по формуле:
А) 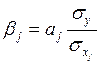 ; б)
; б) 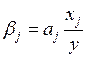 ; в)
; в) 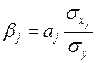 ; г)
; г) 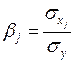
8. Укажите последовательность этапов проведения корреляционно-регрессионного анализа.
А) проверка адекватности построенной модели;
Б) интерпретация полученных результатов;
В) отбор факторов для построения модели;
Г) выбор вида регрессионной модели и оценка ее параметров;
Д) постановка задачи;
Е) сбор исходных данных их анализ.
9. Многофакторная регрессионная модель считается статистически значимой, если
А) Fтабл>Fрасч;
Б) Fтабл=Fрасч;
В) Fтабл<Fрасч.
10.К универсальным показателям тесноты связи относят:
А) парный коэффициент корреляции;
Б) корреляционное отношение;
В) множественный коэффициент детерминации;
Г) индекс корреляции.
11.Надежность модели определяется по:
А) T-статистике Стьюдента;
Б) F-критерию Фишера;
В) коэффициенту детерминации;
Г) средней относительной ошибке аппроксимации.
12.Число наблюдений считается достаточным, когда:
А) n-p-1<30;
Б) n-p+1>30;
В) n-p-1>30;
Г) n-p+1<30.
13.Среднюю относительную ошибку аппроксимации рассчитывают по формуле:
А) ![]() ; б)
; б) ![]() ;
;
В) ![]() ; г)
; г) 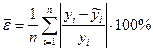 .
.
14.Регрессионная связь – это
А) связь между одной зависимой и несколькими другими, называемыми независимыми переменными, выраженная с помощью математической модели;
Б) связь, при которой на величину исследуемого показателя оказывают множество факторов, действующих в различных направлениях одновременно или последовательно;
В) связь между несколькими зависимыми и независимыми показателями, действующих в различных направлениях одновременно и последовательно.
15.Коэффициент эластичности рассчитывается по формуле:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
16.Коэффициент множественной детерминации показывает, какую часть вариации исследуемого показателя объясняют факторы
А) неучтенные в многофакторной регрессионной модели;
Б) присутствующие в многофакторной регрессионной модели;
В) как присутствующие, так и неучтенные в многофакторной регрессионной модели.
17.Исследование остатков предполагает проверку наличия следующих предпосылок метода наименьших квадратов:
А) отсутствие автокорреляции остатков;
Б) остатки не случайны;
В) гетероскедастичность;
Г) гомоскедастичность;
Д) случайный характер остатков;
Е) наличие зависимости остатков от изменения факторов;
Ж) нулевая средняя величина остатков;
З) остатки подчиняются нормальному закону распределения.
18.Значения частного коэффициента корреляции могут находиться в интервале:
А) [-1; 0];
Б) [0, 4];
В) [-1; 1];
Г) [0; 1].
19.Фиктивные переменные – это
А) независимые переменные;
Б) количественные переменные;
В) качественные переменные;
Г) качественные переменные, преобразованные в количественные.
20.Верные или ложные следующие утверждения:
А) автокорреляция характерна в основном для временных рядов;
Б) статистика Дарбина-Уотсона лежит в пределах от 0 до 4;
В) автокорреляция всегда является следствием неправильной спецификации модели;
Г) при наличии автокорреляции значение коэффициента детерминации R2 будет всегда существенно ниже единицы.
| < Предыдущая | Следующая > |
|---|