1.02. Две переменные: меры . изменчивости и связи

В приводимой ниже таблице 1.2 указаны уровни безработицы (в %) среди белого и цветного населения США в период с марта 1968 г. по июль 1969 г. (месячные данные). В первом столбце расположены номера последовательных наблюдений (Для марта 1968 г., =17 для июля 1969 г.), во втором столбце - значения уровня безработицы среди белого населения в -ом месяце, а в третьем - значения уровня безработицы среди цветного населения в -ом месяце.

Табл. 1.2

I	BEL	ZVET	I	BEL	ZVET
1	3.2	6.9	10	3.0	6.5
2	3.1	6.7	11	3.0	6.0
3	3.2	6.5	12	2.9	5.7
4	3.3	7.1	13	3.1	6.0
5	3.3	6.8	14	3.1	6.9
6	3.2	6.4	15	3.1	6.5
7	3.2	6.6	16	3.0	7.0
8	3.1	7.3	17	3.2	6.4
9	3.0	6.5

Рассмотрим, прежде всего, графики изменения уровней безработицы в обеих группах в течение указанного периода времени (Рис. 1.2).

Первое впечатление от просмотра этих графиков - уровень безработицы среди цветного населения существенно выше и изменяется со временем со значительными колебаниями; уровень безработицы среди белого населения изменяется плавно и в довольно узком диапазоне.

Рис. 1.2

Для того, чтобы использовать обозначения, соответствующие общепринятой практике, мы обозначим через последовательно наблюдаемые уровни безработицы среди цветного населения, а через - соответствующие им уровни безработицы среди белого населения США, так что мы можем говорить о наблюдаемых значениях двух переменных: переменной - уровня безработицы среди цветного населения, и переменной - уровня безработицы среди белого населения.

Наиболее простыми показателями, характеризующими последовательности и , являются их Средние значения (means)

А также Дисперсии (точнее, Выборочные дисперсии - sample variances)

Характеризующие Степень разброса Значений () вокруг своего среднего ( , соответственно), или Вариабельность (Изменчивость) этих переменных на множестве наблюдений. Отсюда обозначение Var (Variance). Впрочем, более естественным было бы измерение степени разброса значений переменных в тех же единицах, в которых измеряется и сама переменная. Эту задачу решает показатель, называемый Стандартным отклонением (Standard deviance - Std. Dev.) переменной (переменной ), определяемый соотношением

(Соответственно).

Вычисления по указанным формулам приводят к значениям =, =; , =. Иными словами, уровень безработицы среди цветного населения, в среднем, более, чем в два раза превышает уровень безработицы среди белого населения. Стандартные отклонения, соответственно, относятся приблизительно как 4:1, что указывает на гораздо более сильную изменчивость (“вариабельность”) уровня безработицы среди цветного населения. Размахи колебаний уровней равны, соответственно, 7.3 - 5.7 = 1.6 и 3.3 - 3.1 = 0.2.

Удобным графическим средством анализа данных является Диаграмма рассеяния (scatterplot), на которой в прямоугольной системе координат располагаются точки , I = 1, 2, ..., N, где N - Количество наблюдаемых пар значений переменных и . В нашем примере N = 17, и диаграмма рассеяния имеет вид

Рис. 1.3

Вытянутость облака точек на диаграмме рассеяния вдоль наклонной прямой позволяет сделать предположение о том, что существует некоторая объективная тенденция Линейной связи между значениями переменных и , выражаемой соотношением

Где — уровень безработицы среди цветного, а — среди белого населения. В то же время, указанное соотношение выражает всего лишь Тенденцию: реально наблюдаемые значения Отличаются от значений на величину

Так что

Последнее соотношение определяет Линейную модель наблюдений, Тогда как соотношение

Определяет Линейную модель связи между рассматриваемыми переменными.

Заметим, однако, что видимая степень проявления вытянутости облака точек на диаграмме рассеяния (при наличии линейной связи между переменными) существенно зависит от выбора единиц измерения переменных и . Поэтому, во-первых, желательно при построении диаграммы выбирать масштабы и интервалы изменения переменных таким образом, чтобы диаграмма имела вид квадрата и чтобы на диаграмме имелись точки, достаточно близко расположенные к каждой из четырех границ квадрата. Во-вторых, желательно иметь какие-то числовые характеристики, которые отражали бы Действительное Наличие вытянутости облака точек вдоль наклонной прямой и Не зависели от шкал, в которых представлены значения переменных.

Одна из характеристик такого рода связана с разбиением диаграммы рассеяния горизонтальной и вертикальной прямыми на 4 прямоугольника.

Разбивающие диаграмму прямые (секущие) проводятся через точку так что если точка лежит правее вертикальной секущей, то отклонение имеет знак плюс, а если левее, то знак минус. Аналогично, если точка лежит выше горизонтальной секущей, то отклонение имеет знак плюс, а если она расположена ниже этой секущей, то знак минус (см. Рис. 1.4).

Рис. 1.4

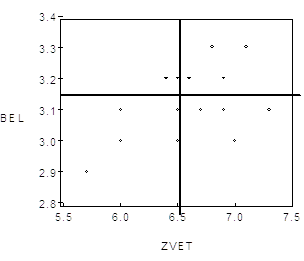
Пусть — количество таких точек среди , для которых и (верхний правый прямоугольник); — Количество точек, для которых и (нижний правый прямоугольник); — количество точек, для которых и (верхний левый прямоугольник); - количество точек, для которых и (нижний левый прямоугольник). В нашем примере, , , (точки, соответствующие наблюдениям с номерами 6 и 17, имеют совпадающие координаты), (точки, соответствующие наблюдениям с номерами 9 и 10, имеют совпадающие координаты), так что количество точек с совпадающими знаками отклонений и равно , а количество точек, у которых знаки отклонений различны, равно .

Количество точек с совпадающими знаками отклонений от средних значений составляет 10/17=0.59, т. е. около 59% общего числа точек, и это служит некоторым указанием на наличие вытянутости облака точек в направлении прямой, имеющей Положительный угловой коэффициент. Если бы большинство составляли точки с противоположными знаками отклонений от средних значений, то это служило бы объективным указанием на наличие вытянутости облака точек в направлении прямой, имеющей Отрицательный угловой коэффициент. Последняя ситуация часто наблюдается при рассмотрении зависимости спроса на товар от его цены.

Более распространенным является определение степени выраженности линейной связи между произвольными переменными и , Принимающими значения и , , посредством (Выборочного) Коэффициента корреляции (Sample correlation coefficient)

Величина Стоящая в числителе, определяется соотношением

И называется (Выборочной) Ковариацией Переменных и , Так что, формально,

Если указанная тенденция выражена на диаграмме рассеяния довольно ясно, то значения по абсолютной величине близки к единице (т. е. значения Близки к +1 или к –1). Если же наличие линейной тенденции связи обнаруживается на диаграмме рассеяния с трудом, то тогда значения близки к нулю. Как мы увидим позднее, значения Уже Не зависят от выбора шкал измерения переменных и (если, конечно, эти шкалы Линейны).

В нашем примере , , , откуда находим

Т. е. получаем значение , расположенное приблизительно посередине между 0 и 1.

Замечание

Мы определили Var И Cov, Деля соответствующие суммы квадратов на N-1. Это имеет свое объяснение, которое пока выходит за рамки нашего обсуждения. Вместе с тем, в разных руководствах по эконометрике Var И Cov Определяются по-разному. Деление на N - 1 используется, например, в книгах Доугерти (1997), Айвазяна и Мхитаряна (1998), тогда как в книге Магнуса, Катышева и Пересецкого (1997) соответствующие суммы квадратов делятся не на N - 1, а на N. К счастью, и Cov И Var будут играть у нас лишь вспомогательную роль, а величина более существенного для нас коэффициента корреляции Rxy не зависит от того, каким из двух способов мы будем определять Var И Cov, Лишь бы только при определении обеих этих характеристик использовался один и тот же способ.

< Предыдущая		Следующая >