Лабораторная работа №2
ФОРМИРОВАНИЕ КОМБИНАТОРНЫХ МНОЖЕСТВ
Цель работы: Получение навыков программирования с использованием рекурсивных функций на основе работы с комбинаторными множествами.
Методические указания
Рекурсивные функции формирования комбинаторных множеств
Рассмотрим рекурсивные функции, которые в качестве выходного параметра возвращают набор комбинаций.
Рекурсивная функция формирования комбинаций перестановок с повторениями:
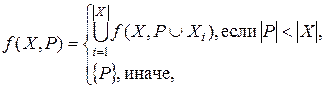
Где X – исходный список чисел,
![]() – число элементов в списке X,
– число элементов в списке X,
P – список перестановок (вначале P=Æ).
Рекурсивная функция формирования комбинаций перестановок:
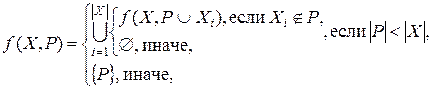
Где X – исходный список чисел,
![]() – число элементов в списке X,
– число элементов в списке X,
P – список перестановок (вначале P=Æ).
Рекурсивная функция формирования комбинаций размещений с повторениями:
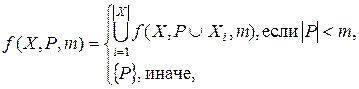
Где X – исходный список чисел,
![]() – число элементов в списке X,
– число элементов в списке X,
P – список перестановок (вначале P=Æ),
M – количество выбираемых элементов из списка X.
Рекурсивная функция формирования комбинаций размещений:
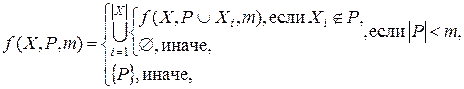
Где X – исходный список чисел,
![]() – число элементов в списке X,
– число элементов в списке X,
P – список перестановок (вначале P=Æ),
M – количество выбираемых элементов из списка X.
Рекурсивная функция формирования комбинаций сочетаний с повторениями:
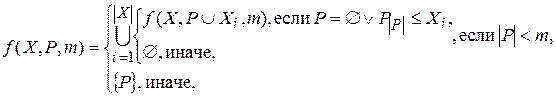
Где X – исходный список чисел (числа расположены в порядке возрастания),
![]() – число элементов в списке X,
– число элементов в списке X,
P – список перестановок (вначале P=Æ),
M – количество выбираемых элементов из списка X.
Рекурсивная функция формирования комбинаций сочетаний:
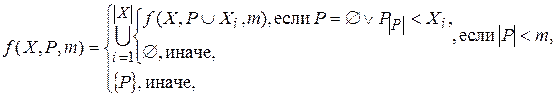
Где X – исходный список чисел (числа расположены в порядке возрастания),
![]() – число элементов в списке X,
– число элементов в списке X,
P – список перестановок (вначале P=Æ),
M – количество выбираемых элементов из списка X.
Рекурсивная функция, возвращающая список операций перемещения N элементов из стека А в стек С через стек В по правилам ханойской башни:
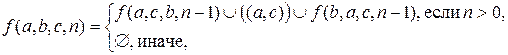
Где (A, B, C) – номера стеков ((A, B, C)=(1, 2, 3)),
N – число элементов в стеках.
Реализация рекурсивных функций формирования комбинаторных множеств в MathCad
Реализация рекурсивной функции формирования комбинаций перестановок с повторениями:
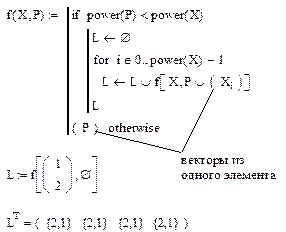
Таким образом, в переменной L будет находиться вектор векторов, которые состоят из двух элементов (MathCad отображает вектор L как вектор состоящий из матриц размером 2´1, т. е. ( {2,1} {2,1} {2,1} {2,1} )). Поместив эти элементы в матрицу, возможно отображение всех комбинаций:

Задание
Ниже приведены варианты заданий. Выполнить задание в MathCad версии 8 или выше. Символы Æ и È взять из файла Symbols. mcd.
A. Ввести пустой список Æ; функцию power(L), возвращающую длину списка L; функцию объединения списков È(A, B) (см. лаб. раб. №1).
Б. Получить список комбинаций (таблица 10.1):
1. Ввести функцию, формирующую список комбинаций.
2. Получить результат функции.
3. Поместить комбинации из списка в матрицу.
Таблица 10.2
|
Вариант |
Вид комбинаций |
Пример |
|
1 |
Перестановки |
Для 4-х элементов |
|
2 |
Размещения с повторениями |
Для 2-х из 4-х элементов |
|
3 |
Размещения |
Для 3-х из 4-х элементов |
|
4 |
Сочетания с повторениями |
Для 3-х из 4-х элементов |
|
5 |
Сочетания |
Для 3-х из 4-х элементов |
|
6 |
Размещения |
Для 4-х из 2-х элементов |
|
7 |
Ханойская башня |
Для 4-х элементов |
|
8 |
Сочетания |
Для 4-х из 2-х элементов |
| < Предыдущая | Следующая > |
|---|