Глава 35. Рекурсивные функции

Алгоритм ставит в соответствие входным данным выходные, следовательно, с каждым детерминированным алгоритмом можно однозначно сопоставить функцию, которую он вычисляет.

Функция, области определения и значений которой есть множество натуральных чисел, называется Вычислимой, если существует машина Тьюринга, которая реализует процесс вычисления значений этой функции.

Попытки описать такие вычислимые функции привели к созданию теории рекурсивной функции.

Рекурсия – это способ задания функций на множестве натуральных чисел, при которых значение функции для произвольного значения аргумента выражаются через значение этой функции при меньшем значении аргумента.

Пример

Рекурсивная функция для вычисления факториала (F(Z) = N!):

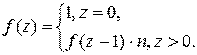
Пример

Рекурсивная функция для вычисления набольшего общего делителя пары чисел (A, B):

< Предыдущая		Следующая >