Глава 21. Нормальные формы
Совершенная дизъюнктивная нормальная форма
В данном разделе на примере булевых функций обсуждается важное понятие «нормальной формы», то есть синтаксически однозначного способа записи формулы, реализующей заданную функцию.
ТЕОРЕМА (О разложении булевой функции по переменным)
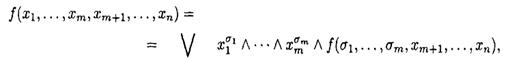
(S1 , … ,SM)
Где дизъюнкция берется по всем возможным наборам (S1 , … ,SM).
Представление булевой функции F(X1, ... ,Xn) в виде
![]()
Называется Совершенной дизъюнктивной нормальной формой (СДНФ).
Пример
X Å Y = XØY Ú ØXy
Минимизация булевых функций
Минимизацией булевых функций называется их представление в виде СДНФ, которая содержит наименьшее число переменных и их отрицаний.
Формула, представленная в виде СДНФ, упрощается многократным применением Операций склеивания
Ab Ú AØB = A
И Операций поглощения
A Ú Ab = A, A Ú ØAb = A Ú B.
Если дальнейшие преобразования невозможны, то говорят, что имеет место Тупиковая форма. Таких форм может быть несколько.
Пример
ØXyØZ Ú ØXyz = ØXy
Графический метод минимизации булевых функций
Рассматриваемый графический метод использует Диаграммы Вейча, которые представляют собой специально организованные таблицы соответствия. Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы также считаются соседними.
Клетки, в которых функция принимает значение 1, заполняются единицами. Соседние клетки, содержащие единицы, объединяются в области. Каждая единица может находиться сразу в нескольких областях, но число областей должно быть минимальным.
Таким образом, каждая полученная область будет соответствовать конъюнкции переменных или их отрицаний (это видно по диаграмме), а сама минимизированная СДНФ будет представлять собой дизъюнкцию этих конъюнкций.
На рисунке 5.1 представлены диаграммы Вейча для функций двух, 3-х, и 4-х переменных. Числа в клетках соответствуют бинарному коду набора значений переменных функции.
|
X1 |
Ø X1 | |
|
X2 |
3 |
1 |
|
Ø X2 |
2 |
0 |
|
X1 |
Ø X1 | |||
|
X3 |
5 |
7 |
3 |
1 |
|
ØX3 |
4 |
6 |
2 |
0 |
|
ØX2 |
X2 |
ØX2 |
|
X1 |
Ø X1 | ||||
|
X3 |
10 |
14 |
6 |
2 |
ØX4 |
|
11 |
15 |
7 |
3 |
X4 | |
|
ØX3 |
9 |
13 |
5 |
1 | |
|
8 |
12 |
4 |
0 |
ØX4 | |
|
ØX2 |
X2 |
ØX2 |
Рис. 5.4. Диаграммы Вейча для функций двух, 3-х, и 4-х переменных
Пример
F(X1, X2) = X1 ® X2 = (1101) – значения функции в таблице истинности.
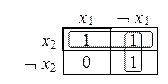
Видно, что первая область соответствует переменной X2 , а вторая ØX1.
Следовательно, F(X1, X2) = X2 Ú ØX1.
Пример
F(X1, X2, X3) = (1001 1100)
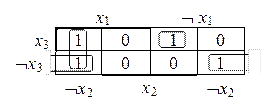
F(X1, X2, X3) = X1ØX2 Ú ØX1X2X3 Ú ØX2ØX3.
Пример
F(X1, X2, X3, X4) = (1011 0110 0111 1111)
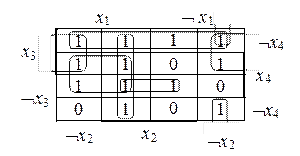
F(X1, X2, X3, X4) = ØX2X3ØX4 Ú X3ØX4 Ú X1X2 Ú ØX1ØX2ØX4 Ú X1X4 Ú X2ØX3 x4.
| < Предыдущая | Следующая > |
|---|