Тема 8 Конечные автоматы

8.1 Детерминированные функции.

8.2 Графическое задание детерминированных функций

8.3 Ограниченно-детерминированные функции.

8.4 Каноническое уравнение ограниченно-детерминированных функций

Автоматом называют дискретный преобразователь информации, способный принимать различные состояния, переходить под воздействием входных сигналов из одного состояния в другое и выдавать выходные сигналы.

Если множество состояний автомата, а так же множество входных и выходных сигналов конечны, то автомат называют конечным автоматом. Все реальные автоматы являются конечными.

Информацию, поступающую на вход автомата, и преобразующую входную информацию принято кодировать конечной совокупностью символов. Эту совокупность называют алфавитом, отдельные символы, образующие алфавит буквами, а любые конечные упорядоченные последовательности букв данного алфавита словами в этом алфавите.

Автоматы функционируют в дискретные моменты времени, которые обозначаются натуральными числами t=0, 1, 2,…. В каждый момент дискретного времени на вход автомата поступает один сигнал (буква), фиксируется определённое состояние автомата и с выхода снимается один сигнал. Реальные автоматы могут иметь, вообще говоря, несколько входов и выходов. В некоторых случаях для решения задач синтеза удобно заменить такие автоматы автоматами с одним входом и одним выходом. Для этого достаточно закодировать соответствующим образом входные и выходные сигналы исходного алфавита. Если, например, автомат имеет два входа, на каждый из которых подаются сигналы 0 или 1, то все возможные комбинации входных сигналов можно закодировать четырьмя буквами (0, 0), (0, 1), (1, 0), (1, 1).

Процесс дискретного преобразования информации автоматами можно описать с помощью детерминированных функций.

8.1 Детерминированные функции. Обозначим через ={0, 1, …, k-1}, где k – некоторое натуральное число, а через множество всех k-значных последовательностей A Таких, что А={A(1), A(2),…,A(t), …}, где A(i) для всех i=1, 2,… .

Обозначим через множество всех функций y=F определённых на наборах , где и принимающие значение из . Функции из преобразуют наборы k-значных последовательностей в k-значные последовательности. В множество включим так же все последовательности из , рассматривая их как функции, зависящие от пустого множества переменных, т. е. как константы.

С помощью векторной записи функции от N переменных из можно свести к функции от одной переменной. Обозначим набор переменных через Х, вместо y=F будем писать y=F (Х). При этом значение переменной Х есть вектор А= компонентами которого являются последовательности из , .Будем рассматривать а как последовательность векторов , где .

Таким образом, мы будем считать, что выполняется тождество: =.

Лемма 1: Число наборов , где равно .

Итак, функцию y=F с помощью векторной записи можно свести к функции y=, где N=. Таким образом, изучение функции y=F из можно свести к изучению функции от одной переменной из , где N=.

Определение 1: Функция y= из называется детерминированной, если какого бы ни было число t и каковы бы ни были последовательности а и b такие, что

A(1)=B(1), A(2)=B(2), … A(t)=B(t) значение функций α, β, где α=, β= представляют собой последовательности, у которых тоже совпадают первые t членов, т. е. α(1)=β(1), α(2)=β(2), …, α(t)=β(t).

Множество всех детерминированных функций обозначим через .

Из определения детерминированной функции следует, что значение α(t) (α=) зависит только от значения первых t членов входной последовательности а, т. е. А(1), А(2), …, А(t), следовательно.

α(t)=φ(А(1), А(2), …, А(t)).

Приведём примеры как детерминированных, так и недетерминированных функций.

Пример 1. Рассмотрим функцию y=, определённую следующим образом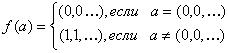

Покажем, что данная функция недетерминированная. Действительно, возьмём две входные последовательности и . Тогда и . Следовательно, данная функция недетерминированная.

Пример 2. Рассмотрим функцию из , определённую следующим образом .Здесь выходная последовательность – почленная конъюнкция входных последовательностей. Очевидно, что .

Пример 3. Рассмотрим функцию z=X+y осуществляющую сложение 2-значных последовательностей в двоичной системе с бесконечным числом разрядов. Для этого используется обычный алгоритм сложения двух чисел столбиком

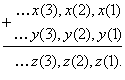
Очевидно, что Z(T) определяется по первым T слагаемых, т. е. X+y.

Детерминированная функция может быть проинтерпретирована следующим образом. Пусть мы имеем некоторый «дискретный преобразователь», в котором существует N Входов и один выход .

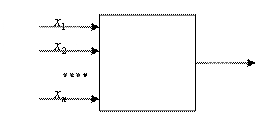
На входы в моменты времени T=1,2,…,M, … подаются входные последовательности

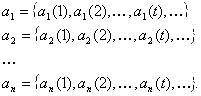
И в эти же моменты T На выходе возникает выходная последовательность , причем . Очевидно, что в дискретном преобразователе значения α(T) Зависит только от значений входных последовательностей в момент времени 1,2,…,T и не зависит от значений в будущие моменты времени. Поэтому преобразование есть детерминированная функция.

8.2 Графическое задание детерминированных функций. Пусть . Выше мы показали, что с помощью векторной записи данную функцию можно свести к функции , где . Рассмотрим бесконечную фигуру:

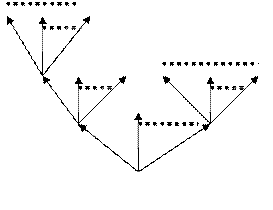
Построена она следующим образом, и называть её будем деревом. Возьмём произвольную вершину , которую назовём корнем дерева. Из неё проведём N рёбер, которые образуют первый ярус. Из концов каждого из рёбер также проведём N рёбер, которые образуют второй ярус и т. д. .Рёбра каждого пучка нумеруются слева направо числами 0,1,…,N-1 или их значениями в k-ичной системе счисления.

В дальнейшем на рисунках номера рёбер будут опускаться. Далее, каждому ребру в построенном дереве произвольным образом припишем одно из чисел множества {0,1,…,k-1}. В результате получим так называемое нагруженное дерево. Рассмотрим следующее нагруженное дерево.

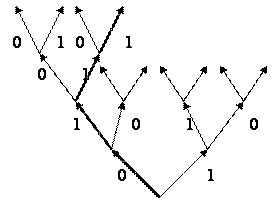
Начиная движение с корня дерева, пойдём по рёбрам. Так, например, последовательности (0,0,1,1…), где числа 0,0,1,1, … - номера рёбер, соответственно, 1-го,2-го,3-го,4-го и т. д. ярусов соответствует выделенный маршрут и последовательность (0,1,1,1…).

Теорема 1: Функция из будет детерминированной тогда и только тогда, когда она может быть заданна с помощью нагруженного дерева.

Доказательство: Покажем, что любое нагруженное дерево задает некоторую детерминированную функцию. Действительно, пусть - произвольная последовательность чисел, где , i=1,2,…. Будем считать, что - номер ребра 1-го яруса, - номер ребра 2-го яруса и т. д. Данной последовательности в нагруженном дереве соответствует единственный маршрут, ведущий из корня дерева. Числа, приписанные выделенным ребрам образуют выходную последовательность . Покажем, что построенная функция из является детерминированной. Пусть и – две входные последовательности такие, что . Ясно, что маршруты в нагруженном дереве, соответствующие данным последовательностям на первых t ярусах совпадают. А это значит, что , т. е. функция детерминированная. Обратное утверждение очевидно. Теорема доказана.

Рассмотрим следующие примеры:

Пример 4. . Ясно, что и число ребер, выходящих из вершин равно . Построим дерево соответствующее данной функции.

. . . . . . . . . .

1 0 1 0 1 0 1 0

1 0 1 0

1 0

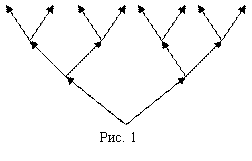
Например, входной последовательности {0,1,1,…} будет соответствовать входная последовательность {1,0,0,…}.

Пример 5. , которая задаётся следующим образом.

, где X(t)·y(t) – конъюнкция.

Для данной функции k=n=2 и число ребер, выходящих из вершин равно N==4. Ребру с номером D=(0,0) соответствует значение (0,0)=0

1=(0,1) 0·1=0

2=(1,0) 1·0=0

3=(1,1) 1·1=1.

Следовательно, данной функции соответствует следующее нагруженное дерево.

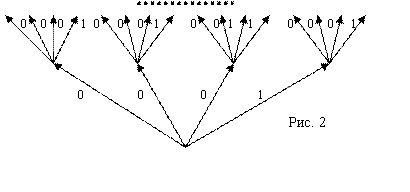
Пример 6. , k=n=1, N==1.

Дерево, соответствующее данной функции строится следующим образом. Процесс приписывания ребрам чисел начинается с 1-го яруса

0=(0,0) 0+0=0

1=(0,1) 0+1=1

2=(1,0) 1+0=1

3=(1,1) 1+1=0

При этом, если появляется перенос в следующий разряд, то конец соответствующего ребра кончается кружочком. Это позволяет выполнить вычисление в следующем ярусе.

8.3 Ограниченно-детерминированные функции. Возьмем нагруженное дерево для некоторой детерминированной функции . Пусть - произвольная его вершина -го яруса. Данную вершину можно рассматривать как корень нагруженного дерева. Согласно теореме 1 оно определяет некоторую детерминированную функцию .

Определение 2. Два поддерева с корнями и исходного дерева называются эквивалентными, если .

Очевидно, что при естественном наложении двух эквивалентных поддеревьев их нумерации совпадают. Так, в дереве Рис.1 и Рис.2 все поддеревья эквивалентны, а в дереве Рис.3 поддеревья с корнями эквивалентны, а с корнями и не эквивалентны.

Определение 3. Весом дерева и весом соответствующей детерминированной функции называется максимальное число попарно неэквивалентных поддеревьев.

Например, все функции из примеров 4,5 равен 1, а из примера 6 равен 2.

Определение 4. Детерминированная функция называется ограниченно – детерминированной функцией, если она имеет конечный вес.

Класс всех ограниченно – детерминированных функций обозначим через

Функции из примеров 4,5,6 являются ограниченно-детерминирован ными функциями.

Рассмотрим следующую детерминированную функцию.

Пример 7. . Ясно, что вес данной функции , т. е. она не является ограниченно-детерминированной.

Пусть , вес которой равен r. Рассмотрим алфавит , который назовём внутренним алфавитом. Каждой вершине нагруженного дерева, соответствующей функции припишем одну из букв алфавита с соблюдением следующего правила: эквивалентным вершинам приписываются одни и те же буквы из . В результате получаем так называемое полное нагруженное дерево.

Для любой ограниченно – детерминированной функции соответствующее ей полное нагруженное дерево можно свести к коечному дереву с занумерованными ребрами и вершинами. Если в нем провести отождествление эквивалентных вершин, то получим так называемую диаграмму Мура. В ней нулём отмечена начальная вершина и ребрам приписаны пары чисел (a, b), первое из которых обозначает номер ребра, а второе число соответствующее этому ребру. Так функция соответствует диаграмме Мура.

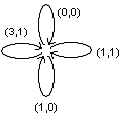
А функция

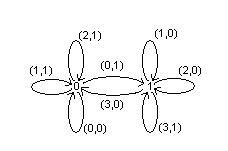
8.4 Каноническое уравнение ограниченно-детерминированных функций. Пусть - ограниченно-детерминированная функция с весом R.

Пусть - входная последовательность. Ей соответствует выходная последовательность и последовательность состояний .

Возьмем другую входную последовательность . Ей соответствуют, соответственно, выходная последовательность и последовательность состояний

В общем случае из того, что не следует, что . Однако, если и , то и . Другими словами это означает, что если два одноименных ребра () выходят из эквивалентных вершин (), то они будут нагружены одной и той же буквой () и входить в эквивалентные вершины (). Это означает, что

(*)

Уравнения (*) называются каноническими уравнениями функции . Первое уравнение называется уравнением выход, второе уравнением перехода.

Уравнение (*) можно задать с помощью канонической таблицы.

X(t)	Q(t-1)	Y(t)	Q(t)

Пусть X(t) и y(t) из {0,1}, а . Если вес r≤2, то каноническая таблица есть таблица истинности. Если r>2, то каноническая таблица не является таблицей истинности. Но с помощью кодирования всех чисел алфавита в двоичной системе счисления мы её можем преобразовать в таблицу истинности.

Рассмотрим теперь функцию от n переменных с весом r>1, - внутренний алфавит. Закодируем все числа из алфавита в двоичной системе счисления наборами из {0,1} длинной . В этом случае канонические уравнения искомой функции имеют вид.

(**)

В дальнейшем договоримся, что начальные состояния в канонических уравнениях (**) Q(0)=0, а в уравнениях (*) .

Пример 8. Найти канонические уравнения функции

Ранее мы показали, что вес данных функций равен 2 и её диаграмма Мура

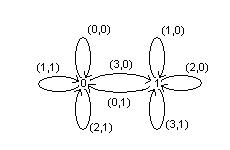
Построим каноническую таблицу.

X(t)

Y(t)

Q(t-1)

Z(t)

Q(t)

Данная каноническая таблица является таблицей истинности.

Запишем канонические уравнения, используя результаты раздела 3.

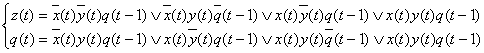
Используя законы алгебры логики

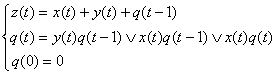
Пример 9. Найти каноническое уравнение для функции заданной следующей диаграммой Мура

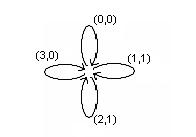
Строим каноническую таблицу.

X(t)

Y(t)

Q(t-1)

Z(t)

Q(t)

Отсюда

Заметим, что если вес функции равен 1, то в канонических уравнениях будет отсутствовать.

Пример 10. Найти канонические уравнения ограничено-детерминированой функции заданной следующей диаграммой Мура: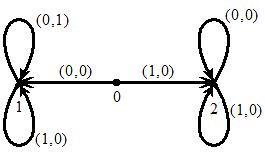

Ясно, что вес данной функции равен 3. Построим каноническую таблицу для данной функции:

X(t)

Q(t-1)

Y(t)

Q(t)

Данная таблица не является таблицей истинности. Преобразуем данную таблицу в таблицу истинности. Для этого значения второго и четвёртого столбца закодируем в двоичной системе счисления:

X(t)

Y(t)

Не определена

Доопределим данную функцию следующим образом:

X(t)

Y(t)

Составим канонические уравнения используя аппарат булевой алгебры:

Y(t)=

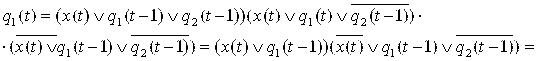
Итак, искомые канонические уравнения имеют вид:

Каждой ограниченно-детерминированной можно сопоставить канонические уравнения. Однако выбор канонических уравнений не однозначен. Эта неоднозначность связана:

1) с различными способами кодирования состояний.

2) с различными способами доопределения функций.

Очевидно, что канонические уравнения позволяют вычислить

По входной последовательности A={A(1),A(2),…,A(t),…}

Выходную последовательность B={B(1),B(2),…,B(t),…}.

Итак, для задания конечного автомата фиксируется три конечных множества (алфавита):

– множество возможных входных сигналов

– множество возможных выходных сигналов

– множество возможных внутренних состояний автомата

На этих множествах задаются две детерминированные функции

– функцию переходов Ψ, определяющую состояние автомата Q(t) дискретного времени t в зависимости от состояния автомата Q(t-1) и значения входного сигнала в момент времени t.

Q(t)= Ψ(X(t),Q(t-1))

– функцию выходов Ф, определяющую зависимость выходного сигнала автомата y(t) от состояния автомата Q(t-1) и входного сигнала X(t) в момент времени t.

Y(t)=Ф(X(t),Q(t-1))

Кроме того на множестве состояний автомата фиксируется одно из внутренних состояний Q(0) в качестве начального состояния.

Вопросы для самоконтроля

1. Дайте определение детерминированной функции.

2. Приведите примеры детерминированных функций.

3. Приведите примеры недетерминированных функций.

4. Приведите графическую интерпретацию детерминированных функций.

5. Что такое бесконечное нагруженное дерево?

6. Что такое вес бесконечно нагруженного дерева?

7. Какие функции называются ограниченно детерминированными?

8. Приведите примеры ограниченно детерминированных функций.

9. Приведите примеры неограниченно детерминированных функций.

10. Что такое диаграмма Мура?

11. Дайте определение канонических уравнений ограниченно детерминированных функций.

< Предыдущая		Следующая >