Тема 5 Контактные и логические схемы

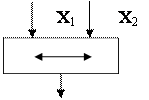
В начале прошлого века известный физик П. Эренфест впервые указал на возможность применения аппарата алгебры логики в технике. Эта идея нашла свое воплощение в работах советского физика В. И.Шестакова, американского математика К. Шеннона и японского инженера А. Какасима. Первыми объектами применения алгебры логики для решения технических задач были контактные схемы. Под контактными схемами мы будем понимать электрические цепи, содержащие только контакты. Каждый контакт может находиться в двух состояниях – разомкнут (0) и замкнут (1). Такие цепи мы будем изображать диаграммой, на которой возле контактов пишется или . Причем значение 1 этих переменных соответствует прохождению тогда через данный контакт, а значение 0 нет.

Если контакты X и y соединены последовательно, то цепь замкнута, когда оба контакта замкнуты и разомкнуты, когда хотя бы один из контактов разомкнут. Ясно, что такой схеме

Соответствует булева функция .

Если контакты X и y соединены параллельно то цепь замкнута, когда хотя бы один контакт замкнут и разомкнут, когда оба контакта разомкнуты. Ясно, что такой схеме

Соответствует булева функция .

Указанное соответствие позволяет любую булеву функцию представить в виде контактной схемы. С другой стороны, любая контактная схема с последовательно или параллельно соединенными контактами реализуется булевой функцией. Задача анализа контактной схемы и состоит в построении соответствующей ей булевой функции.

Например, контактная схема

Реализуется булевой функцией .

Однако, поскольку одна и та же булева функция может быть выражена различными формулами, то ее реализация контактными схемами неоднозначна. Всегда можно построить много различных контактных схем, соответствующих данной функции. Такие схемы называют эквивалентными. Задача синтеза контактной схемы состоит в построении контактной схемы по заданной булевой функции, которая может быть задана как формулой, так и таблицей. В обоих случаях необходимо выразить функцию через операции конъюнкции, дизъюнкции и отрицания. Каждая операция конъюнкции соответствует последовательному соединению контактов. В результате параллельного соединения получаем контактную схему. Из множества эквивалентных схем, путем упрощения формул выделяют наиболее простую схему. Центральной проблемой синтеза контактных схем является построение для данной булевой функции более простой схемы. Часто эта проблема сводится к минимизации булевых функций, т. е. к такому их представлению, в котором соответствующие формулы содержат минимальное количество вхождений переменных.

Рассмотрим схему

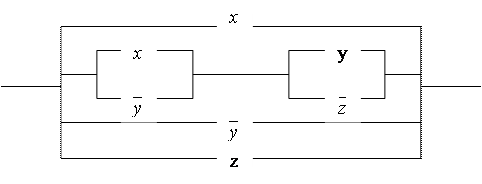
Данная схема реализуется следующей формулой:

Упростим данную формулу. Используя закон дистрибутивности, получаем:

==

Следовательно, данную схему можно упростить, заменив ее следующей эквивалентной схемой:

Решим теперь следующую задачу: из контактов составить по возможности более простую схему так, чтобы она замкнулась тогда и только тогда, когда замкнуты не менее двух контактов.

Составим таблицу истинности для булевой функции, соответствующей требуемой контактной схеме

X	Y	Z
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Найдем для данной булевой функции совершенную ДНФ:

Упростим данную формулу

==.

Данной формуле соответствует следующая контактная схема:

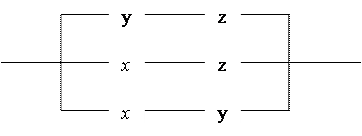
Контактные схемы исторически были первыми техническими средствами реализации булевых функций. В дальнейшем появилось много различных устройств, реализующих булевы функции. Одной и нескольких переменных.

Пусть имеется некоторое устройство, имеющее n упорядоченных «входов» и один «выход», причем внутренняя структура этого устройства нас не интересует. На каждый из входов могут подаваться два сигнала, которые мы будем обозначать символами 0 и 1. При каждом наборе сигналов на входах и выходе возникает один из сигналов 0 или 1. Причем набор сигналов на входах однозначно определяет сигнал на выходе. Очевидно, что каждое такое устройство реализует булеву функцию.

Устройства, реализующие элементарные булевы функции, называются Логическими элементами. Логические элементы изображаются в виде прямоугольников, внутри которых помещаются условные названия или символы соответствующих функций

Функция	Графическое изображение	Функция	Графическое изображении

Из данных логических элементов путем соединения входа одного из них с выходов другого можно строить все более сложные логические схемы. Для полученных таким образом схем легко записывают соответствующие им булевы функции.

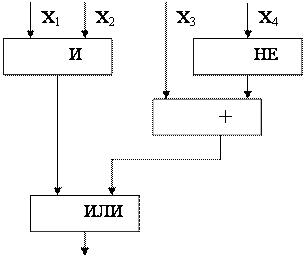
Например, схема

Реализуется булевой функцией

Нетрудно для любой булевой функции построить реализующую ее логическую схему.

Например, булева функция реализуется логической схемой

Рассмотрим построение логической схемы на примере одноразрядного сумматора, выполняющего арифметическое сложение двоичных чисел и , к-го разряда и переноса из младшего разряда . Пусть - получаемая сумма, а - перенос в старший разряд, тогда получаем следующую таблицу истинности такого сумматора.

 

0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Отсюда получаем

Построим схему, соответствующую данному сумматору. Для этого вначале упростим выражение для . Как легко заметить, выражение для не упрощается, используя предыдущие методы. Для упрощения выражения функции используем выражение функции .

Поэтому будем рассматривать как переменную величину. В результате получаем следующую таблицу, которая содержит избыточные наборы переменных:

0	0	0	0	0
0	0	0	1
0	0	1	0	1
0	0	1	1
0	1	0	0	1
0	1	0	1
0	1	1	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1
1	0	1	0
1	0	1	1	0
1	1	0	0
1	1	0	1	0
1	1	1	0
1	1	1	1	1

Отсюда

Используя методы, которые будут рассмотрены в разделе 6, нетрудно упростить выражение для :

=,

Где .

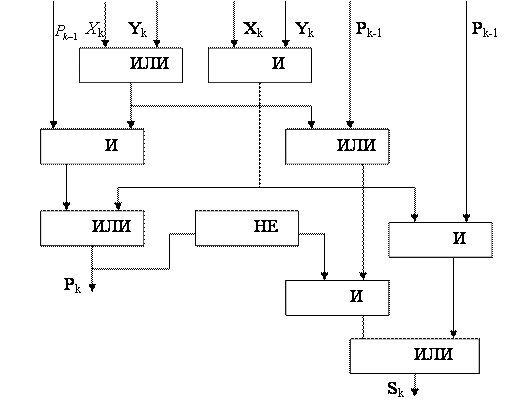
Теперь строим логическую схему:

< Предыдущая		Следующая >