06. Метод вариации произвольной постоянной (метод Лагранжа)

Рассмотрим однородное уравнение

(или ).

Получили уравнение с разделяющимися переменными и поэтому, разделив пе­ременные и вычислив интегралы от обеих частей равенства:

Получим общее решение вида .

Решение данного уравнения ( ) ищем в виде

. (2)

Отсюда

, (3)

Где - произвольная постоянная. Подставляя из (3) в (2), находим общее решение (1):

.

Пример 1. Решить уравнение

(1)

Решение. Рассмотрим однородное уравнение

, (2)

Имеем уравнение с разделяющимися переменными

.

Разделим переменные

И проинтегрируем обе части равенства

- общее решение (2).

Решение исходного уравнения (1) находим в виде

. (3)

Подставив это выражение и его производную в (1), получим:

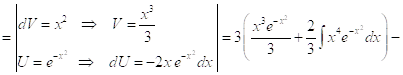
Таким образом

. (4)

Подставим (4) в (3), получим общее решение данного уравнения (1):

.

Пример 2. Решить дифференциальное уравнение

.

Решение. Интегрируем соответствующее однородное уравнение

.

Разделим переменные

.

Интегрируя обе части, находим общее решение однородного уравнения:

.

Варьируем постоянную и решение исходного уравнения ищем в виде

.

Подставляя в исходное уравнение, получим:

Или

.

Таким образом общее решение исходного уравнения имеет вид

.

< Предыдущая		Следующая >