03. Метод изоклин

Метод изоклин – это метод графического решения дифференциального уравнения. Семейство изоклин дифференциального уравнения (1) определяется уравнением

, где - параметр.

Метод изоклин заключается в построении семейства изоклин с нанесен­ными на них отрезками касательных.

Множество отрезков касательных образует поле направлений касатель­ных интегральных кривых. Главное соединение касательных дает семейство интегральных кривых.

Рассмотрим примеры.

Пример 1. Решить методом изоклин уравнение

.

Решение. Данное уравнение опреде­лено во всей плоскости , исклю­чая точки прямых и . В об­ласти определения его можно записать в виде:

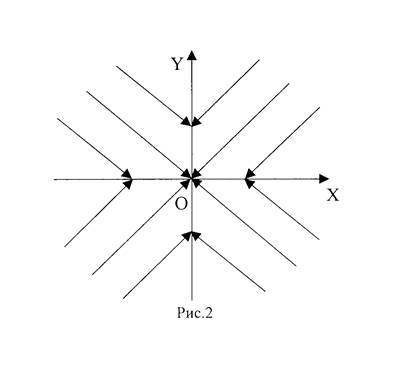
Поэтому в I и II квадрантах координатной плоскости интегральные кривые – это графики функций , а во II и IV квадрантах – графики функций (см. рис.2).

Пример 2. Решить методом изоклин уравнение:

.

Решение. Уравнение изоклины . В данном случае уравне­ние изоклины совпадает с уравне­нием нормали .

Запишем несколько уравнений изоклин для фиксированных угловых коэффи­циентов касательных, если

На рис.3 поле направлений касательных дает семейство интегральных кривых в виде окружностей.

Дифференциальное уравнение вида

,

В котором коэффициенты при дифференциалах распадаются на множители, за­висящие только от и только от , называется уравнением с разделяющимися переменными.

Путем деления на произведение оно приводится к уравнению с разделенными переменными:

.

Общий интеграл этого уравнения имеет вид:

.

Пример 1. Решить уравнение

.

Решение. Представим данное уравнение в виде

.

Разделив обе части этого уравнения на произведение , получим уравнение с разделенными переменными

.

Интегрируя это уравнение, последовательно находим

.

Используя метод подстановки, вычислим интегралы

.

Решением данного дифференциального уравнения является функция:

.

Пример 2. Найти частное решение уравнения

,

Удовлетворяющее начальному условию .

Решение. Найти частные решения данного дифференциального уравнения – это значит решить задачу Коши.

А) Найдем общее решение данного уравнения. Запишем его иначе

.

Данное уравнение является уравнением с разделяющимися переменными. Раз­делим обе части этого уравнения на , получим:

.

Интегрируем:

.

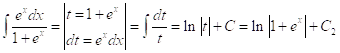Таким образом общий интеграл имеет вид :

Б) Найдем частное решение, для этого определим значение постоянной При данных начальных условиях ; будем иметь

Следовательно .

Подставив найденное значение в общее решение, получим частное решение данного дифференциального уравнения

,

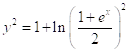Откуда

.

Из начального условия следует, что (т. к. ), поэтому перед корнем берем знак плюс. Итак, искомое частное решение:

.

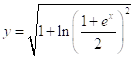< Предыдущая		Следующая >