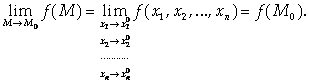3.1.4. Предел и непрерывность функции нескольких переменных
Введем понятие D-окрестности точки М0 (Х0 , у0) на плоскости ОХу как круга радиуса D с центром в данной точке. Аналогично можно определить D-окрестность в трехмерном пространстве как шар радиуса D с центром в точке М0 (Х0 , у0 , Z0). Для N-мерного пространства будем называть D-окрестностью точки М0 множество точек М С координатами ![]() , удовлетворяющими условию
, удовлетворяющими условию
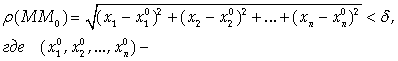
Координаты точки М0. Иногда это множество называют «шаром» в N-мерном пространстве.
|
Число А называется Пределом функции нескольких переменных
В точке М0, если
Такое, что | F(M) – A| < ε для любой точки М из δ-окрестности М0. |
Обозначения:
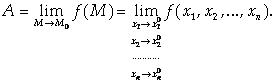
Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри D-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых Повторных пределов, получаемых последовательными предельными переходами по каждому аргументу в отдельности.
Примеры.
1. Покажем, что функция ![]()

Не имеет предела при М, стремящемся к О(0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую У = х, то на этой прямой
![]()
Если же траекторией движения считать прямую У = 2Х, то
![]()
Следовательно, предел в точке (0,0) не существует.
2. Найдем повторные пределы функции

Если же произвести предельные переходы в обратном порядке, получим:
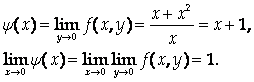
Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле).
Замечание. Можно доказать, что из существования предела в данной точке в обычном смысле и существования в этой точке пределов по отдельным аргументам следует существование и равенство повторных пределов. Обратное утверждение неверно.
|
Функция
Называется Непрерывной в точке М0 Если
|
Если ввести обозначения
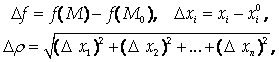
То это условие можно переписать в форме
![]()
|
Внутренняя точка М0 Области определения функции Z = F (M) называется Точкой разрыва функции, если в этой точке не выполняется условие
|
Замечание. Множество точек разрыва может образовывать на плоскости или в пространстве Линии Или Поверхности разрыва.
Примеры.
1. Функция Z = X² + Y² непрерывна в любой точке плоскости ОХу. Действительно,

Поэтому
![]()
2. Единственной точкой разрыва функции
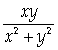
Является точка (0,0).
3. Для функции
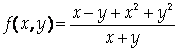
Линией разрыва является прямая х + у = 0.
| < Предыдущая | Следующая > |
|---|