2.7.4. Примеры решения задач по теме «Выпуклость. Асимптоты»

Задача 1.

Найти интервалы выпуклости функции

Указание

Функция выпукла при условии

Решение

Область определения функции:

Ответ:

Задача 2.

Найти интервалы вогнутости функции

Указание

Границами интервалов выпуклости и вогнутости могут быть не только точки, в которых вторая производная равна нулю, но и точки, в которых она не существует.

Решение

Область определения функции:

Представим вторую производную в виде:

И исследуем знак полученного выражения. Корень знаменателя: Х = 2. Найдем корень числителя.

Знак второй производной:

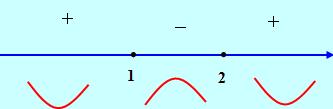
Рис. 8

Следовательно, интервалы вогнутости:

Ответ:

Задача 3.

Найти точки перегиба функции

Указание

В точках перегиба вторая производная меняет знак, то есть требуется найти точки, в которых У’’ = 0 или не существует.

Решение

Область определения функции:

Проверим, меняется ли знак второй производной в найденных точках.

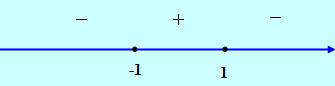
Рис. 9

Значит, Х = +1 – точки перегиба.

Ответ: Х = +1.

Задача 4.

При каких значениях А и B точка (-2,0) служит точкой перегиба линии

Указание

Для определения А и B требуется решить систему

Решение

Для того чтобы (-2,0) была точкой перегиба, нужно, чтобы Y’’(-2)=0.

При этом точка (-2,0) лежит на кривой, то есть У(-2)=0. Подставим в это равенство B = 6A:

Ответ: А = 1, B = 6.

Задача 5.

Сколько асимптот имеет график функции

Указание

График имеет вертикальные асимптоты, если

Условие наличия горизонтальной асимптоты – конечный предел

Если этот предел бесконечен, функция может иметь наклонную асимптоту при условии, что

Решение

Исследуем функцию на наличие асимптот разных видов.

1) х = +1 – точки разрыва 2-го рода, поэтому прямые Х = +1 – горизонтальные асимптоты графика.

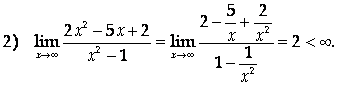
Следовательно, прямая У = 2 – горизонтальная асимптота графика на обоих концах оси Ох. При этом наклонных асимптот у функции быть не может.

Итак, график имеет 3 асимптоты (две вертикальных и одну горизонтальную).

Ответ: 3.

Задача 6.

Асимптоты какого вида имеет график функции

Указание

График имеет вертикальные асимптоты, если

Условие наличия горизонтальной асимптоты – конечный предел

Если этот предел бесконечен, функция может иметь наклонную асимптоту при условии, что

Решение

1)Точка разрыва функции: Х = 0. При этом

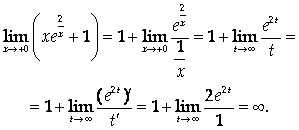
Если хотя бы один из односторонних пределов в данной точке бесконечен, через точку проходит вертикальная асимптота. Значит, Х = 0 – вертикальная асимптота графика.

Следовательно, горизонтальных асимптот нет.

Значит, прямая У = х + 3 – наклонная асимптота графика.

Ответ: график имеет вертикальную и наклонную асимптоту.

< Предыдущая		Следующая >