2.6.1. Монотонность и экстремумы

Функция Y = F(X) называется Возрастающей (убывающей) на [Ab], если

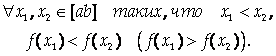
Теорема 1. Если функция F(X), дифференцируемая на [Ab], возрастает на этом отрезке, то на [Ab].

Если F(X) непрерывна на [Ab] и дифференцируема на (Ab), причем для A < X < B, то эта функция возрастает на отрезке [Ab].

Доказательство.

1. Пусть F(X) возрастает на [Ab]. Тогда при

Если же

Следовательно, в обоих случаях

Значит,

Что и требовалось доказать.

2. Пусть

По теореме Лагранжа

Но по условию

Следовательно, F(X) – возрастающая функция.

Замечание 1. Аналогичную теорему можно доказать и для убывающей функции: если F(X) убывает на [Ab], то на [Ab]. Если на (Ab), то F(X) убывает на [Ab].

Замечание 2. Геометрический смысл доказанной теоремы: если функция возрастает на отрезке [Ab], то касательная к ее графику во всех точках на этом отрезке образует с осью Ох острый угол (или горизонтальна).

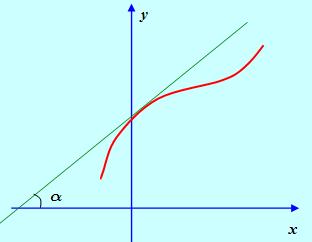
Рис. 1

Если же функция убывает на рассматриваемом отрезке, то касательная к графику этой функции образует с осью Ох тупой угол (или в некоторых точках параллельна оси Ох).

Рис. 2

< Предыдущая		Следующая >