2.5.2. Формы остаточного члена в формуле Тейлора
Покажем, что Rn(X) = O(X-A)N. Из выбора многочлена Pn(X) следует, что
![]() Применив для вычисления предела
Применив для вычисления предела
![]()
N раз правило Лопиталя, получим:

Утверждение доказано. Представление остаточного члена в виде Rn = O(X-A)N
Называется записью остаточного члена В форме Пеано.
Найдем еще один вид записи Rn(X). Представим его в виде
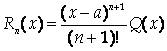
И определим вид функции Q(X). Из формулы Тейлора следует, что

Пусть при заданных значениях Х и А Q(X)=Q. Рассмотрим вспомогательную функцию от T (A < T < X):

При этом предполагается, что А И Х приняли фиксированные значения. Тогда
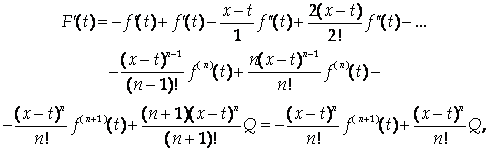
То есть F(T) дифференцируема в окрестности точки А. Из предыдущих выкладок следует, что F(X) = F(A) = 0, поэтому к функции F(T) можно применить теорему Ролля: существует T = X (A < X < X) такое, что F’(X) = 0. Тогда
![]()
Откуда Q = F(N+1) (X). Используя это выражение, получим запись остаточного члена В форме Лагранжа:

Так как A < X < X, можно представить X = а + Q(Х – а), где 0 < Q < 1. При этом
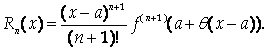
Замечание. Если в формуле Тейлора принять А = 0, этот частный случай называют Формулой Маклорена:

| < Предыдущая | Следующая > |
|---|