2.2.3. Производная обратной функции

Если для функции y=f(x) существует обратная функция х=j(у), которая в некоторой точке у имеет производную j’(у)≠0, то в соответствующей точке х функция f(x) тоже имеет производную, причем

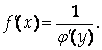
Доказательство.

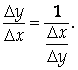
Так как j(у) непрерывна,

И при переходе к пределу при Получаем:

< Предыдущая		Следующая >