2.1.8. Примеры решения задач по теме «Производная и дифференциал»

Задача 1.

Найти приращение функции

В точке Х0 = -3, если приращение независимой переменной DХ = 0,3.

Указание

Найдите разность значений У (-3+0,3) и У (-3).

Решение

Ответ: -3,42.

Задача 2.

Найти приращение независимой переменной DХ, для которого приращение функции

В точке Х0 = 4 равно

Указание

Решите уравнение

Решение

По определению приращения функции

Следовательно, DХ можно найти из уравнения

Ответ: -0,76.

Задача 3.

Вычислить значение производной функции

В точке Х0 = -1.

Указание

По определению производной

Решение

Ответ: 1.

Задача 4.

Найти угловой коэффициент касательной к графику функции

Указание

Угловой коэффициент касательной к графику функции равен значению производной функции в точке касания.

Решение

Найдем производную данной функции в точке касания:

Следовательно, угловой коэффициент касательной к графику функции при равен 3.

Ответ: 3.

Задача 5.

Составить уравнение касательной к графику функции

В точке с абсциссой Х0 = 3.

Указание

Уравнение касательной к графику функции Y = F (X) в точке с абсциссой Х0 имеет вид

Решение

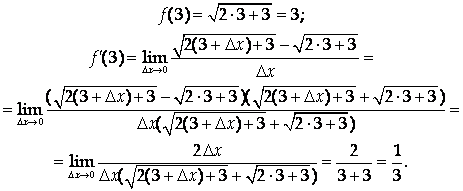
Следовательно, уравнение касательной имеет вид:

Ответ:

Задача 6.

Найти угол, под которым пересекаются кривые

Указание

Угол между кривыми в точке их пересечения определяется как угол между касательными к ним, проведенными в этой точке.

Решение

Найдем абсциссу точки пересечения кривых:

Вычислим их производные при Х = 1:

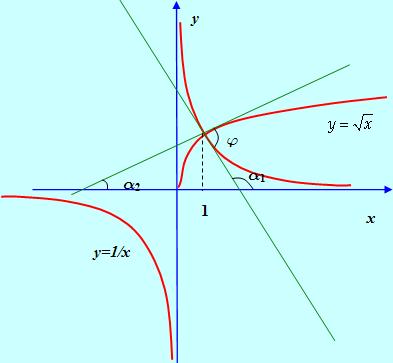
Если A1 и A2 – углы, образованные касательными к графикам данных функций при Х = 1 с осью Ох, то тангенс угла J между касательными ( и соответственно между кривыми) можно найти по формуле тангенса разности:

Ответ: arctg 3.

< Предыдущая		Следующая >