1.4.6. Примеры решения задач по теме «Непрерывность функции»
Задача 1.
При каком значении числа А функция
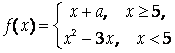
Будет непрерывной?
Указание
Функция может иметь разрыв только в точке Х = 5, поэтому А следует выбрать так, чтобы в этой точке выполнялось равенство
![]()
Областью определения функции является все множество действительных чисел, причем по обе стороны точки Х = 5 функция является элементарной, то есть непрерывной. Для обеспечения непрерывности в точке Х = 5 поставим условие
![]()
Ответ: 5.
Задача 2.
Каким числом можно доопределить функцию
![]()
При Х = 0, чтобы она стала непрерывной в этой точке?
Указание
Подобная операция возможна в том случае, если точка разрыва является устранимой особенностью, то есть существует конечный предел функции в этой точке.
Найдем предел данной функции в точке Х = 0:
![]()
Следовательно, если принять F (0) = 3, функция станет непрерывной точке Х = 0.
Ответ: 3.
Задача 3.
Каким числом можно доопределить функцию
![]()
При Х = 0, чтобы она стала непрерывной в этой точке?
Указание
Вычисляя предел функции в точке Х = 0, воспользуйтесь тем, что второй множитель – ограниченная функция, и примените свойства бесконечно малых.
Решение

Ограниченная функция. Как известно, произведение бесконечно малой функции на ограниченную есть бесконечно малая, поэтому
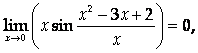
То есть предел существует и конечен. Поэтому можно доопределить функцию так: F (0) = 0.
Ответ: F (0) = 0.
Задача 4.
Каким числом можно доопределить функцию
![]()
При Х = 0, чтобы она стала непрерывной в этой точке?
Указание
Подобная операция возможна в том случае, если точка разрыва является устранимой особенностью, то есть существует конечный предел функции в этой точке.
Решение

Найдем односторонние пределы данной функции в точке Х = 0:

Следовательно, предел данной функции в точке Х = 0 в обычном смысле не существует, поэтому добиться ее непрерывности в этой точке невозможно.
Ответ: это невозможно.
Задача 5.
Найти количество точек разрыва функции
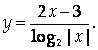
Исследовать характер этих точек.
Указание
На область определения накладываются два ограничения: логарифмируемое выражение должно быть положительным, а знаменатель дроби – не равным нулю.
Решение
Данная функция не существует при трех значениях аргумента: Х = 0 и Х = +1 (в первом случае знаменатель не существует, во втором он равен нулю). Каждая из найденных точек является внутренней точкой области определения и, следовательно, точкой разрыва.
Исследуем характер точек разрыва:

Следовательно, Х = 0 – устранимая особенность.
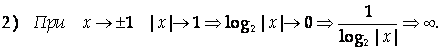
Следовательно,

И Х = +1 – точки разрыва 2-го рода.
Ответ: Х = 0 – устранимая особенность, Х = +1 – точки разрыва 2-го рода.
Задача 6.
Выяснить, какие из функций

Имеют точки разрыва 1-го рода.
Указание
В точке разрыва 1-го рода существуют конечные односторонние пределы функции, но они не равны между собой.
Решение
Найдем точки разрыва каждой функции и исследуем их характер.
1) Функция
![]()
Не определена при Х = 0.
![]()
Следовательно, единственная точка разрыва этой функции – это точка разрыва 2-го рода.
2) Функция
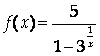
Не определена при Х = 0 (заметим, что знаменатель основной дроби не равен нулю ни при каком значении Х).
Найдем односторонние пределы F (X) в точке Х = 0:

Следовательно, Х = 0 – точка разрыва 1-го рода.
3) Функция

Не определена при Х = 5.

Следовательно, точка Х = 5 – точка разрыва 2-го рода.
4) Функция
![]()
Не определена при Х = -0,5. При этом

Таким образом, односторонние пределы в точке Х = -0,5 равны соответственно 1 и -1, то есть эта точка – точка разрыва 1-го рода.
Ответ: 2,4.
| < Предыдущая | Следующая > |
|---|