1.3.3. Примеры решения задач по теме «Сравнение бесконечно малых»

Задача 1.

Определить порядок малости относительно Х функции

Указание

Представьте функцию в виде произведения двух множителей, один из которых – бесконечно малая при а второй имеет в точке Х = 0 конечный предел.

Решение

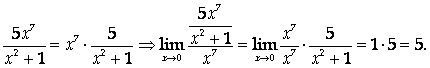
Следовательно, данная функция – бесконечно малая одного порядка с Х7.

Ответ: 7.

Задача 2.

Определить порядок малости относительно Х функции

Указание

Воспользуйтесь таблицей эквивалентных бесконечно малых.

Решение

Следовательно, данная бесконечно малая эквивалентна Х, то есть имеет порядок, равный 1.

Ответ: 1.

Задача 3.

Вычислить предел, воспользовавшись таблицей эквивалентных бесконечно малых:

Указание

Используйте соотношения эквивалентности:

Решение

Воспользуемся соотношениями эквивалентности:

Тогда

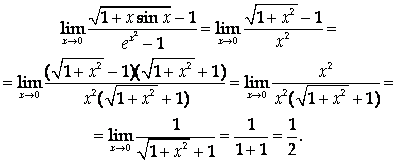
Ответ:

Задача 4.

Вычислить предел, воспользовавшись таблицей эквивалентных бесконечно малых:

Указание

Используйте соотношения эквивалентности:

Решение

Воспользуемся соотношениями эквивалентности:

Тогда

Задача 5.

Вычислить предел, воспользовавшись таблицей эквивалентных бесконечно малых:

Указание

Используйте соотношения эквивалентности:

Решение

Воспользуемся соотношениями эквивалентности:

Тогда

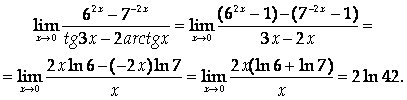
Ответ:

Задача 6.

Даны неограниченные функции при

Определите, какие из них являются бесконечно большими.

Указание

Используйте связь бесконечно малых и бесконечно больших функций: если F (X) – бесконечно малая при то при этом – бесконечно большая, и определение бесконечно большой функции:

Решение

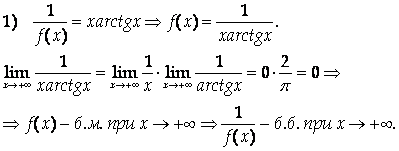
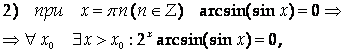
Что противоречит определению бесконечно большой функции.

Как известно, произведение бесконечно малой на ограниченную есть бесконечно малая, следовательно, F (X) – бесконечно большая.

Что противоречит определению бесконечно большой функции.

Ответ: 1,3.

< Предыдущая		Следующая >