1.3.2. Бесконечно большие функции

Функция f(x) называется бесконечно большой при хХ0, если

Для бесконечно больших можно ввести такую же систему классификации, как и для бесконечно малых, а именно:

1. Бесконечно большие f(x) и g(x) считаются величинами одного порядка, если

2. Если

То f(x) считается бесконечно большой более высокого порядка, чем g(x).

3. Бесконечно большая f(x) называется величиной k-го порядка относительно бесконечно большой g(x), если

Замечание.

Отметим, что ах – бесконечно большая (при а>1 и ) более высокого порядка, чем xk для любого k, а logax – бесконечно большая низшего порядка, чем любая степень хk.

Теорема.

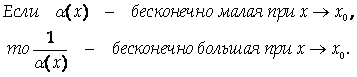
Доказательство.

Докажем, что

Для этого достаточно выбрать в качестве e 1/M. Тогда

Следовательно,

То есть 1/α(х) – бесконечно большая при

< Предыдущая		Следующая >