1.2.2. Основные теоремы о пределах

Теорема 1. Если существуют

То существует и

Доказательство.

Используя третье определение предела, представим F(X)=A+A(X), G(X)=B+B(X), где A(х) и B(х) – бесконечно малые при . Тогда F(X)+G(X)=A+B+(A(X)+B(X))=A+B+G(X), где G(х)=A(х)+B(х) – бесконечно малая. Следовательно,

Теорема 2. Если существуют

То существует и

Доказательство.

Представим f(x)=A+a(x), g(x)=B+b(x), где a(х) и b(х) – бесконечно малые при . Тогда f(x)·g(x)=AB+Ab(x)+Ba(x)+a(x)b(x). Но Ab(x)+Ba(x)+a(x)b(x) – бесконечно малая (так как f(x) и g(x) ограничены в окрестности х0), следовательно,

Теорема 3. Если существуют

То существует и

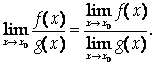
Доказательство.

Представим f(x)=A+a(x), g(x)=B+b(x), где a(х) и b(х) – бесконечно малые при . Тогда

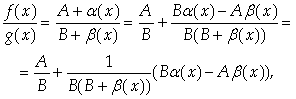
Где Ограниченная в окрестности х0 функция, так как имеет предел, равный 1/В², а Вa(х)-Аb(х) – бесконечно малая. Поэтому

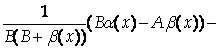
Бесконечно малая, и

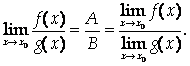
Теорема 4 («лемма о двух милиционерах»). Если f(x) ≤ j(x) ≤ g(x) в некоторой окрестности х0 и

То существует и

Доказательство.

Из условия теоремы следует, что

Выберем d-окрестность точки х0, в которой

Тогда

Поэтому |j(x)-A|<e, следовательно,

Теорема 5. Если

Доказательство.

Предположим, что А<0. Тогда, выбрав e=|A|/2, найдем окрестность точки х0, в которой |f(x)-A|<|A|/2, следовательно, 3А/2<f(x)<A/2, то есть f(x)<0 в рассматриваемой окрестности, что противоречит условию теоремы.

Следствие 1.

Аналогично доказывается, что если f(x)≤0, то А≤0.

Следствие 2.

Если f(x)≥g(x) и обе функции имеют пределы в точке х0, то

Замечание. Все перечисленные утверждения можно доказать для

Теорема 6 (без доказательства). Ограниченная и возрастающая при a<x<b (a<x<) функция имеет предел при

< Предыдущая		Следующая >