1.1. Понятие функций нескольких переменных
В науке и технике часто приходится встречаться с одновременным, совместным изменением нескольких переменных, связанных между собой некоторыми условиями. Так площадь прямоугольника 
изменяется с изменением длин его сторон 
и 
, объем цилиндра 
изменяется с изменением радиуса основания 
и высоты цилиндра 
.
Пусть дано некоторое множество 
пар чисел 
.
Функцией двух переменных называется соответствие, при котором каждой паре чисел 
соответствует единственное число 
.
При этом 
и 
называются Независимыми переменными (или Аргументами), 
- Зависимой переменной (или Функцией), множество - Областью определения функции, а 
- множеством значений функции.
Обозначения функции двух переменных аналогичны обозначениям функции одной переменной: 
, 
, 
и т. д.
При нахождении частного значения 
функции , которое она принимает при заданных численных значениях аргументов 
и 
, пишут 
или 
. Например, если 
, то 
.
Так как каждой паре чисел соответствует единственная точка 
плоскости 
и обратно, каждой точке соответствует единственная пара чисел , то функцию двух переменных можно рассматривать как функцию точки . Поэтому вместо записи 
пишут 
. в этом случае областью определения функции является некоторое множество 
точек плоскости .
В основном мы будем рассматривать функции двух переменных, однако все сказанное целиком переносится и на функции любого числа переменных, которые определяются аналогичным образом.
Функцией трех переменных называют соответствие, при котором каждой тройке 
соответствует единственное число 
.
При этом , и Называют Независимыми переменными (или Аргументами), 
- Зависимой переменной (или Функцией), множество 
- областью определения функции, а 
- множеством значений функции.
Функцию трех переменных обозначаются так же, как и функции одной или двух переменных: 
, 
и т. д.
Функцию трех переменных можно рассматривать как функцию точки 
, имеющей координаты , , в пространственной системе координат 
.
Область определения функции есть некоторое множество точек в пространстве.
Аналогично можно ввести Понятие функции четырех, пять и вообще 
переменных.
Функцию переменных 
также рассматривают как функцию точки 
- мерного пространства и пишут 
.
Если функция задана аналитическим выражением, причем область определения функции заранее не указана, то в качестве области определения принимают совокупность всех тех точек 
, для которых данное аналитическое выражение имеет конечное действительное значение.
Пример 1. Найти область определения функции
.
Решение. Областью определения этой функции является множество всех точек, для которых выражение 
определено, т. е. множество точек, для которых 
, или 
, т. е. внутренность круга с центром в начале координат и радиусом, равным 1 (рис. 1).
Пример 2. Найти область определения функции 
.
Решение. Областью определения этой функции является множество точек, удовлетворяющих условию 
, или 
, т. е. все точки плоскости за исключением точек прямой 
(рис. 2).
Пример 3. Найти область определения функции
.
Решение. Функция будет принимать действительные значения при условии, что 
, или 
. То есть область определения функции является шар радиуса 2 с центром в начале координат. Точки граничной шаровой поверхности относятся к области определения функции.
Пусть функция определена в некоторой области на плоскости . Тогда каждой точке будет соответствовать точка 
трехмерного пространства.
Множество всех таких точек , , называется Графиком функции . В общем случае графиком функции является Поверхность в пространстве.
В аналитической геометрии уже рассматривались некоторые поверхности, которые являются графиками функций двух переменных.
Например, эллиптический параболоид является графиком функции 
.
Линией уровня называется множество точек на плоскости , в которых функция принимает данное постоянное значение 
. Эту линию можно также получить, пересекая график функции плоскостью 
, параллельной плоскости , и проектируя линию пересечения ортогонально на плоскость (рис. 3).
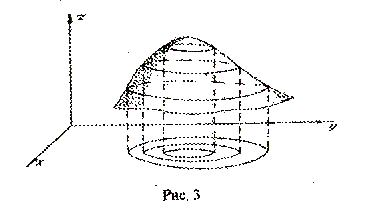
Система линий уровня 
, где 
, позволяет судить о ходе изменения функции. Там, где линии уровня располагаются густо, функция изменяется быстро, а где линии уровня расположены редко, функция изменяется медленно.
Пример 4. Найти линии уровня функции 
.
Решение. Рассмотрим
,
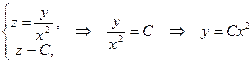Т. е. линиями уровня является семейство парабол.
Для функции трех переменных рассматривают Поверхности уровня – множество точек пространства, в которых функция принимает данное постоянное значение.
| Следующая > |
|---|
