14. Методы решения задач на условный экстремум
1°. Метод исключения переменных состоит в том, что из - условий связи ![]() переменных выражаются через остальные
переменных выражаются через остальные ![]() , и задача на условный экстремум функции
, и задача на условный экстремум функции ![]() переменных приводится к задаче на экстремум для функции
переменных приводится к задаче на экстремум для функции ![]() переменных.
переменных.
Метод применяют для задач небольшой размерности.
2°. Метод неопределенных множителей Лагранжа позволяет избежать трудностей, связанных с выражением одних переменных через другие.
Метод состоит в следующем:
1. Составляют функцию Лагранжа:
 .
.
2. Стационарные точки функции Лагранжа и коэффициенты ![]() находят из системы
находят из системы ![]() уравнений
уравнений
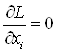 ,
, ![]() ;
;
 ,
, ![]() .
.
Стационарные точки функции Лагранжа совпадают со стационарными точками функции ![]() из множества
из множества ![]() .
.
3. Для установления, являются ли стационарные точки точками экстремума, в каждой стационарной точке вычисляют второй дифференциал функции Лагранжа:
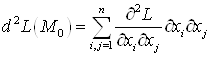 .
.
4. При установлении знака ![]() следует помнить, что
следует помнить, что ![]() связаны уравнениями
связаны уравнениями 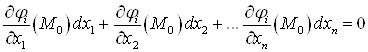 ,
, ![]() .
.
Примеры
1. Исследовать на экстремум функцию ![]() при условии, что
при условии, что ![]()
Решим поставленную задачу методом неопределенных множителей Лагранжа:
1) Составим функцию Лагранжа
2) ![]() Система, из которой определяется множитель l и критические точки, имеет вид:
Система, из которой определяется множитель l и критические точки, имеет вид:

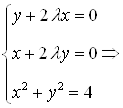
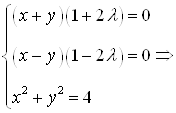
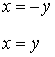

![]()
 .
.
Система определяет 4 стационарные точки:
![]()
![]()
![]()
![]() .
.
Первым двум точкам ![]() соответствует
соответствует ![]() ; точкам
; точкам ![]() —
— ![]()
3) ![]()
![]()
![]()
![]()
![]()
4) Дифференцируя условие связи, получаем соотношение, связывающее ![]() и
и ![]()
![]()
В точках ![]() :
: ![]()
![]()
![]() точки
точки ![]() — точки условного минимума.
— точки условного минимума.
![]()
В точках ![]() :
: ![]()
![]()
![]() точки
точки ![]() — точки условного максимума.
— точки условного максимума.
![]()
5°. В некоторых случаях исследование знака второго дифференциала не обязательно. В приведенном выше примере непрерывная функция ![]() рассматривается на ограниченном замкнутом множестве, определяемом условием:
рассматривается на ограниченном замкнутом множестве, определяемом условием: ![]()
Такая функция достигает наибольшего и наименьшего значений. Поскольку в стационарных точках ![]() функция принимает только 2 различных значения:
функция принимает только 2 различных значения: ![]() и
и ![]() , то без исследования знака второго дифференциала очевидно, что
, то без исследования знака второго дифференциала очевидно, что ![]() — точки минимума,
— точки минимума, ![]() — точки максимума.
— точки максимума.
В некоторых задачах геометрического характера, достаточно найти стационарную точку. Характер экстремума следует из самого смысла задачи.
2. На плоскости ![]() найти точку, сумма квадратов расстояний от которой до точек А(1, 1,1) и В(2, 3, 4) была бы наименьшей.
найти точку, сумма квадратов расстояний от которой до точек А(1, 1,1) и В(2, 3, 4) была бы наименьшей.
Пусть ![]() — искомая точка. Тогда выражение
— искомая точка. Тогда выражение ![]() представляет собой сумму квадратов расстояний от точки
представляет собой сумму квадратов расстояний от точки ![]() до точек
до точек ![]() и
и ![]() . Поскольку
. Поскольку ![]() принадлежит плоскости, то ее координаты удовлетворяют уравнению плоскости:
принадлежит плоскости, то ее координаты удовлетворяют уравнению плоскости: ![]()
Итак, речь идет об исследовании на экстремум функции
![]() при условии
при условии
![]()
1) Составим функцию Лагранжа:
![]()
2) Система для определения стационарных точек имеет вид:
3)


![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Итак, точка  — единственная стационарная точка.
— единственная стационарная точка.
По геометрическому смыслу задача не имеет максимума.
Значит  — искомая точка минимума.
— искомая точка минимума.
| < Предыдущая | Следующая > |
|---|