09. Геометрически приложения. Задача о нахождении наибольших и наименьших значений

1°. Пусть пространственная кривая задана параметрически: ; где — дифференцируемые функции.

В тех точках , где , кривая имеет касательную. Уравнение касательной:

.

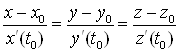2°. Нормальной плоскостью к кривой в т. называется плоскость, проходящая через эту точку перпендикулярно касательной.

Её уравнение:

3°. Пусть поверхность задана уравнением , — точка поверхности, тогда уравнение касательной плоскости имеет вид:

4°. Прямая, проходящая через т. перпендикулярно касательной плоскости, называется нормалью к поверхности.

Уравнение нормали:

.

Примеры.

А) На линии найти точку, касательная в которой параллельна плоскости Написать уравнение касательной.

Решение: по условию касательная параллельна плоскости, а значит, вектор касательной перпендикулярен нормальному вектору плоскости .

; .

Искомая точка имеет координаты ; ; а уравнение касательной

.

Б) Для поверхности найти уравнение касательной плоскости, параллельной плоскости .

Решение:

Уравнение искомой касательной плоскости

,

Поскольку касательная плоскость параллельна плоскости , то координаты их нормальных векторов пропорциональны

;

Подставляя эти соотношения в уравнение поверхности, получим

; ,

Таким образом, есть 2 точки, удовлетворяющие условию: а уравнения касательных плоскостей

1.

1.

В) Доказать, что касательная плоскость к поверхности в любой точке образует с координатными плоскостями тетраэдр постоянного объема.

Решение:

Пусть — произвольная точка поверхности

; ; ;

Уравнение касательной

,

.

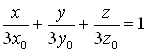Отрезки, отсекаемые касательной плоскостью на осях координат, соответственно равны Объем тетраэдра равен

5°. Наибольшее и наименьшее значение функции в области

Функция дифференцируемая в ограниченной замкнутой области, достигает своего наибольшего (наименьшего) значения либо в стационарной точке, либо на границе области.

Для решения задачи о наибольшем (наименьшем) значении нужно:

1) Найти стационарные точки функции , попадающие внутрь области.

Для этого нужно решить систему уравнений .

2) Выбрать те стационарные точки, которые попали внутрь области. Вычислить значение функции в этих точках.

3) Найти наибольшее и наименьшее значение функции на границе области. Эта задачи сводится к отысканию наибольшего и наименьшего значения функций одной переменной.

4) Сравнивая все полученные значения, найти наибольшее и наименьшее из них.

Пример.

Найти наибольшее и наименьшее значения функции в области, ограниченной осями координат и прямой

Решение:

Указанная область — треугольник АОВ. В соответствии с приведенной схемой решения

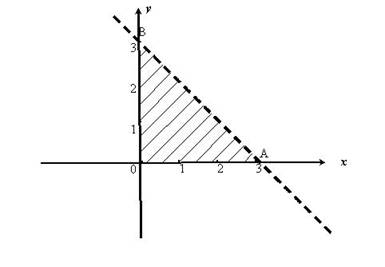
Находим стационарные точки функции:

, .

2) Точка является внутренней точкой области; .

3) Исследуем функцию на границе области:

: . Задача сводится к отысканию наибольшего и наименьшего значений функции одной переменой , .

Находим . Точка — стационарная точка этой функции;

В граничных точках и значения функции равны , .

Аналогично на прямой : , , Точка — стационарная, принадлежит области В граничной точке ,

На отрезке прямой

— стационарная точка,

На концах отрезка значения функции уже вычислены.

4) Выбирая наименьшее и наибольшее из всех полученных значений, находим:

,

< Предыдущая		Следующая >