05. Полный дифференциал функции нескольких переменных. Дифференцирование сложных и неявных функций
1°. Полным приращением функции называется разность 
2°. Функция 
называется дифференцируемой в т. 
, если ее приращение 
может быть представлено в виде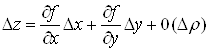 
.
Достаточным признаком дифференцируемости является непрерывность частных производных.
3°. Главная часть полного приращения функции , линейная относительно DX и DY называется ее полным дифференциалом и обозначается 
.
Дифференциалы независимых переменных X и Y совпадают с их приращениями: 
; 
.
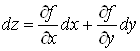4°. В пространстве Rn для функции F (X1, ... Xn) полный дифференциал является линейной формой относительно 
.
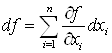
5°. При достаточно малых приращениях аргументов полное приращение функции приближенно равно ее дифференциалу 
.
Этот факт используется в приближенных вычислениях.
Примеры:
А) Найти полное приращение функции 
в т. 
.
Б) Найти полный дифференциал функции 
В) Заменяя приращение функции ее полным дифференциалом, вычислить приближенно 
А) По определению полного приращения функции в точке 
В нашем случае 
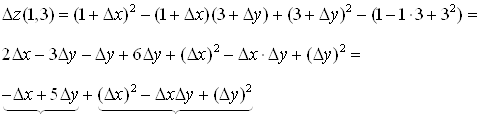
Первая часть линейна относительно 
; 
; вторая — при 
, 
является бесконечной малой более высокого порядка малости, чем первая.
Б)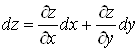 
Находим частные производные
,
,
.
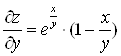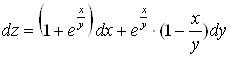В) Рассмотрим функцию 
.
При 
имеем 
;
Находим полный дифференциал функции в произвольной точке
.
Вычисляем полный дифференциал в точке (1, 2) при данных приращениях:
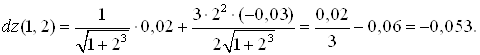
Тогда 
.
6°. Если функция 
дифференцируема в т. 
, а функции 
и 
дифференцируемы в т. , то сложная функция 
дифференцируема в т. и ее частные производные находят по формулам:
,
.
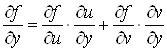7°. Если 
, то полная производная 
вычисляется по формуле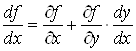 
8°. Если функция зависит от переменных 
непосредственно и как сложная функция 
, то следует различать частную производную, учитывающую непосредственную зависимость от переменных 
и 
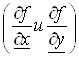и частную производную, учитывающую как непосредственную зависимость, так и через функции 
и 
,
.
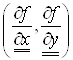
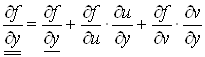Примеры:
А) Найти частные производные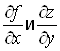 
функции 
, если 
.
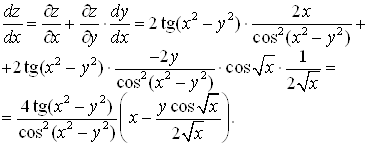
Б) Найти производную 
функции 
, если 
.
А) — сложная функция переменных 
и 
.
Б) Функция зависит от переменной непосредственно и через функцию 
9°. Если функция задана неявно уравнением 
и 
, то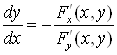 
.
Если функция двух переменных 
задана неявно уравнением
и 
то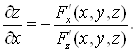 
; 
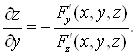
Примеры:
А) Вычислить производную функций, заданной неявно уравнениями
Решение: функция y (x) задана неявно уравнением
.
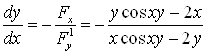Б) Функция задана неявно уравнениями
Найти ее частные производные в т. 
.
Решение:
,
,
,
,
; 
;
; 
.
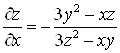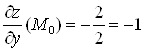| < Предыдущая | Следующая > |
|---|