1. Числовая последовательность и ее предел
Определение 1. Если каждому натуральному числу ![]() по определённому правилу ставится в соответствие число
по определённому правилу ставится в соответствие число ![]() , то множество чисел
, то множество чисел ![]() называется числовой последовательностью.
называется числовой последовательностью.
Определение 2. Числа, из которых составлена последовательность, называют её членами.
Задать числовую последовательность – значит, задать правило, с помощью которого по номеру члена можно найти этот член, т. е. задать функцию ![]() , где
, где ![]() – правило соответствия между
– правило соответствия между ![]() и
и ![]() , а
, а ![]() .
.
Определение 3. Общим членом последовательности называется её ![]() –й член
–й член ![]() , записанный в виде функции от
, записанный в виде функции от ![]() , т. е.
, т. е. ![]() .
.
Если ![]() задано, то последовательность имеет вид
задано, то последовательность имеет вид ![]() . Последовательность нельзя задать указанием нескольких её первых членов.
. Последовательность нельзя задать указанием нескольких её первых членов.
Определение 4. Числовая последовательность, у которой все члены равны между собой, называется постоянной последовательностью или просто постоянной.
Пример 1. ![]() , т. е.
, т. е. ![]() .
.
Пример 2. ![]() , т. е.
, т. е. ![]() .
.
Числовая последовательность – частный случай дискретной переменной величины ![]() , принимающей значение
, принимающей значение ![]() . Эта переменная упорядочена, так как если
. Эта переменная упорядочена, так как если ![]() , то
, то ![]() предшествует
предшествует ![]() .
.
Определение 5. Постоянное число ![]() называется пределом числовой последовательности
называется пределом числовой последовательности ![]() , если для всякого
, если для всякого ![]() можно указать такой номер
можно указать такой номер ![]() , начиная с которого все последующие члены последовательности удовлетворяют неравенству
, начиная с которого все последующие члены последовательности удовлетворяют неравенству
![]() . (1)
. (1)
Записывается это так: ![]() при
при ![]() или
или ![]() (читают: «
(читают: «![]() стремится к
стремится к ![]() при
при ![]() , стремящемся к бесконечности, или предел
, стремящемся к бесконечности, или предел ![]() при
при ![]() , стремящемся к бесконечности, равен
, стремящемся к бесконечности, равен ![]() »).
»).
Неравенство (1) можно переписать в виде
![]()
Или ![]() . (2)
. (2)

Рисунок 1
Определение 6. Интервал (промежуток) ![]() называется
называется ![]() – окрестностью точки
– окрестностью точки ![]() . (рис.1)
. (рис.1)
Пользуясь понятием ![]() – окрестности, определение предела числовой последовательности можно сформулировать следующим образом: число
– окрестности, определение предела числовой последовательности можно сформулировать следующим образом: число ![]() есть предел последовательности
есть предел последовательности ![]() , если можно указать такой номер
, если можно указать такой номер ![]() , что все члены последовательности с номерами большими
, что все члены последовательности с номерами большими ![]() , находятся в
, находятся в ![]() – окрестности точки
– окрестности точки ![]() , где
, где ![]() – любое как угодно малое положительное число
– любое как угодно малое положительное число ![]() . Иначе говоря, все члены последовательности с номерами, большими
. Иначе говоря, все члены последовательности с номерами, большими ![]() , на оси
, на оси ![]() (см. рис.1) изображаются точками, лежащими от точки
(см. рис.1) изображаются точками, лежащими от точки ![]() на расстоянии, меньшем
на расстоянии, меньшем ![]() .
.
Определение 7. Последовательность, имеющая предел, называется сходящейся.![]()
Определение 8. Последовательность, не имеющая предела, называется расходящейся.
Пример 3. Доказать, что предел последовательности с общим членом ![]() равен
равен ![]() , т. е.
, т. е. ![]() .
.
Решение. По определению предела последовательности число 2 будет пределом данной последовательности, если для любого ![]() укажем такой номер
укажем такой номер ![]() , что для всех членов последовательности с номерами
, что для всех членов последовательности с номерами ![]() будет выполняться неравенство
будет выполняться неравенство
![]() , или
, или  .
.
Пусть задано положительное число ![]() , тогда из последнего неравенства находим
, тогда из последнего неравенства находим ![]() , или
, или ![]() . Если теперь в качестве
. Если теперь в качестве ![]() взять любое натуральное число, не меньше
взять любое натуральное число, не меньше ![]() , то при всех
, то при всех ![]() для любого
для любого ![]() будет выполняться неравенство
будет выполняться неравенство
![]()
![]() , или
, или  ;
;
Значит, по определению ![]() .
.
Пусть, например, ![]() , тогда
, тогда  и
и ![]() . Возьмем любой член данной последовательности с номером, большим 19, например
. Возьмем любой член данной последовательности с номером, большим 19, например ![]() , и найдём значение
, и найдём значение 
 .
.
Если ![]() , то
, то 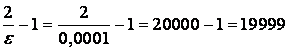 и
и ![]() . Возьмём член последовательности с номером, большим
. Возьмём член последовательности с номером, большим ![]() , например
, например
![]() ,
,
И найдём значение
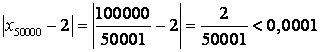 .
.
Для любого ![]() , пользуясь выражением
, пользуясь выражением ![]() , можно подобрать натуральное число
, можно подобрать натуральное число ![]() такое, что все члены последовательности с номерами, большими
такое, что все члены последовательности с номерами, большими ![]() , будут, находится в
, будут, находится в ![]() –окрестности числа 2, а это значит (по определению), что
–окрестности числа 2, а это значит (по определению), что ![]() .
.
Ответ: ![]() .
.
Пример 4. Доказать, что последовательность
![]()
С общим членом

Предела не имеет.
Решение. Легко установить, что точки ![]() с нечетными номерами «стягиваются» к точке 0, а точки
с нечетными номерами «стягиваются» к точке 0, а точки ![]() с четными номерами – к точке 1. Следовательно, любая окрестность точки 0, а также любая окрестность точки 1 содержит бесконечное множество точек
с четными номерами – к точке 1. Следовательно, любая окрестность точки 0, а также любая окрестность точки 1 содержит бесконечное множество точек ![]() . Пусть
. Пусть ![]() есть произвольное действительное число. Всегда можно выбрать настолько малое
есть произвольное действительное число. Всегда можно выбрать настолько малое ![]() , чтобы
, чтобы ![]() –окрестность точки
–окрестность точки ![]() не содержала по крайней мере некоторую окрестность одной из точек 0 или 1, тогда вне этой окрестности будет находиться бесконечное множество чисел
не содержала по крайней мере некоторую окрестность одной из точек 0 или 1, тогда вне этой окрестности будет находиться бесконечное множество чисел ![]() и поэтому нельзя утверждать, что все числа
и поэтому нельзя утверждать, что все числа ![]() , начиная с некоторого, попадут в
, начиная с некоторого, попадут в ![]() –окрестность точки
–окрестность точки ![]() . А это значит, по определению, что число
. А это значит, по определению, что число ![]() не является пределом данной последовательности. Но число
не является пределом данной последовательности. Но число ![]() – произвольное, поэтому никакое число не является пределом этой последовательности.
– произвольное, поэтому никакое число не является пределом этой последовательности.
| Следующая > |
|---|