6.6. Интерполяционные методы Адамса

При S = 1 формула (6.16) примет вид

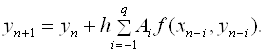(6.22)

Если Q = 2, получим следующее вычислительное правило:

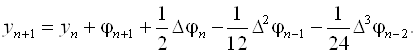(6.23)

Обычно на практике используют экстраполяционную формулу (6.18), а затем корректируют полученное значение по формуле (6.23). И если результат уточненного значения не превышает допустимую погрешность расчета, то шаг H считается допустимым .

Для расчетов на компьютере формулы (6.18) и (6.23) в конечно-разностном виде неудобны. С учетом (6.21) их можно представить в виде

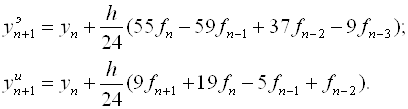(6.24)

Приведенные формулы имеют достаточно большую точность. Они дают погрешность порядка ~ О( H4 ), но сами формулы оценки погрешности достаточно сложны. Приближенно погрешность можно оценить по правилу Рунге.

Пример 6.2. Решить дифференциальное уравнение 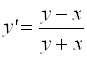на отрезке [0, 1] c начальным условием Y(X=0) = 1. Найти решение методом Адамса (с коррекцией) в точке X4, решение в трех первых точках найти методом Рунге- Кутта, приняв шаг .

Решение. Значения функции в четырех первых точках возьмем из табл. 6.1 (см. пример в предыдущем разделе). Теперь стало понятно, зачем мы сохраняли значения первой производной в этих точках (см. формулы (6.24)).

X4 = X3 + H = 0.15 + 0.05 = 0.2;

Для того чтобы скорректировать полученный результат, необходимо вычислить значение производной в этой точке:

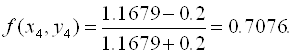
Теперь уточним значение по интерполяционной формуле (а можно этого и не делать, тогда погрешность метода будет больше):

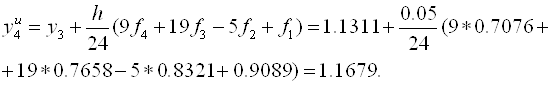
Так как в качестве нового значения функции принято скорректированное, то Обязательно Следует пересчитать значение производной. В нашем случае модуль разности экстраполяционной и интерполяционной формул меньше ε, Что позволяет продолжить вычисления с тем же шагом.

Вопросы для самопроверки

· Сформулируйте задачу Коши для обыкновенных дифференциальных уравнений первого порядка.

· Что является решением дифференциального уравнения: а) в высшей математике, б) в прикладной математике?

· Какие методы решения дифференциальных уравнений называются одношаговыми, многошаговыми? Приведите примеры.

· Сравните решения, полученные на первом, втором шаге методами Эйлера, Рунге-Кутта и разложением в ряд Тейлора (трудоемкость, погрешность…).

· Как оценить погрешность применяемого метода? Как ее уменьшить?

· Сравните одношаговые и многошаговые методы решения дифференциальных уравнений, указав достоинства и недостатки первых и вторых.

· Что такое экстраполяционные и интерполяционные методы (формулы) Адамса?

· Можно ли применять: а) только экстраполяционные методы Адамса,
б) только интерполяционные?

· Можно ли использовать: а) многошаговые методы без одношаговых;
б) одношаговые методы без многошаговых?

· При решении дифференциального уравнения методом Адамса на 27-м шаге необходимо сменить шаг. Как это сделать?

< Предыдущая		Следующая >