3.8. Метод скорейшего спуска (градиента) для случая . системы линейных алгебраических уравнений
В рассматриваемом ниже итерационном методе вычислительный алгоритм строится таким образом, чтобы обеспечить минимальную погрешность на шаге (максимально приблизиться к корню).
Представим систему линейных уравнений в следующем виде:
 (3.38)
(3.38)
Запишем выражение (3.38) в операторной форме:
![]() (3.39)
(3.39)
Здесь приняты следующие обозначения:
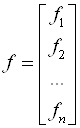 ;
; ![]() ;
;  . (3.40)
. (3.40)
В методе скорейшего спуска решение ищут в виде
![]() , (3.41)
, (3.41)
Где ![]() и
и ![]() - векторы неизвестных на P и P+1 шагах итераций; вектор невязок на P-ом шаге определяется выражением
- векторы неизвестных на P и P+1 шагах итераций; вектор невязок на P-ом шаге определяется выражением
![]() , (3.42)
, (3.42)
А  (3.43)
(3.43)
В формуле (3.43) используется скалярное произведение двух векторов, которое определяется следующей формулой:
 (3.44)
(3.44)
В формуле (3.43) ![]() - транспонированная матрица Якоби, вычисленная на P-ом шаге. Матрица Якоби вектор – функции F(X) определяется как
- транспонированная матрица Якоби, вычисленная на P-ом шаге. Матрица Якоби вектор – функции F(X) определяется как
 (3.45)
(3.45)
Нетрудно убедиться, что для системы (3.39) матрица Якоби равна
 (3.46)
(3.46)
Как и для метода простой итерации, достаточным условием сходимости метода градиента является преобладание диагональных элементов. В качестве нулевого приближения можно взять ![]() .
.
Замечания
· Как видно из выражения (3.45), матрица Якоби не зависит от шага итерации.
· Требования минимизации погрешности на каждом шаге обусловили то, что метод градиента более сложен (трудоемок), чем методы Якоби и Зейделя.
· В методе градиента итерационный процесс естественно закончить при достижении ![]() , вектор невязок входит в вычислительную формулу.
, вектор невязок входит в вычислительную формулу.
Обсуждение
· В приближенных методах можно обеспечить практически любую погрешность, если итерационный процесс сходится.
· Итерационный процесс можно прервать на любом K–ом шаге и продолжить позднее, введя в качестве нулевого шага значения X(K).
· В качестве недостатка приближенных методов можно отметить то, что они часто расходятся, достаточные условия сходимости (преобладание диагональных элементов) можно обеспечить только для небольших систем из 3 – 6 уравнений.
Пример 3.7. Методом скорейшего спуска решим систему уравнений
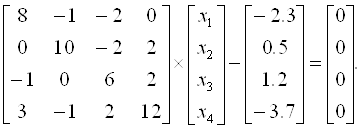
Так как диагональные элементы матрицы являются преобладающими, то в качестве начального приближения выберем:
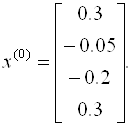
Следовательно, вектор невязок на нулевом шаге равен

Далее последовательно вычисляем
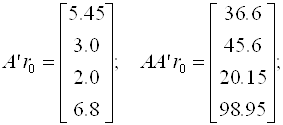
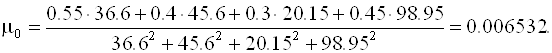
Отсюда 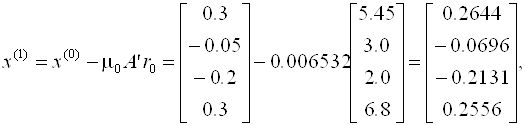
Причем
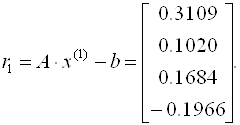
Аналогично находятся последующие приближения и оцениваются невязки. Что касается данного примера, можно отметить, что итерационный процесс сходится достаточно медленно (невязки уменьшаются).
Вопросы для самопроверки
· Назовите известные вам методы решения СЛАУ.
· Чем точные методы отличаются от приближенных?
· Что такое прямой и обратный ход в методе Гаусса?
· Нужен ли обратный ход при вычислении методом Гаусса а) обратной матрицы; б) определителя?
· Что такое невязка?
· Сравните достоинства и недостатки точных и приближенных методов.
· Что такое матрица Якоби?
· Надо ли пересчитывать матрицу Якоби на каждом шаге итерации в методе градиента?
· Исходная СЛАУ решается независимо тремя методами – методом Якоби, методом Зейделя и методом градиента. Будут ли равны значения
А) начального приближения (нулевой итерации);
Б) первой итерации?
· При решении СЛАУ (n > 100) итерационными методами решение расходится. Как найти начальное приближение?
| < Предыдущая | Следующая > |
|---|