10. Уравнение прямой, проходящей через две данные точки

Через две не совпадающие между собой точки можно провести прямую, и притом только одну. Отыщем уравнение прямой, проходящей через точки И .

Предположим, что , т. е. прямая не параллельна оси . Так как прямая проходит через точку , то ее уравнение имеет вид

, (1)

Где - неизвестный угловой коэффициент этой прямой. Но так как прямая проходит также через точку , то координаты и этой точки должны удовлетворять уравнению (1). Отсюда

Следовательно, при имеем

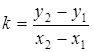. (2)

Подставляя выражение (2) для углового коэффициента в уравнение (1), получим уравнение прямой :

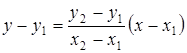. (3)

Это уравнение при можно записать также в виде пропорции

. ()

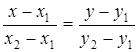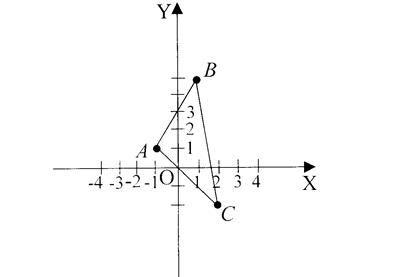Пример. Дан треугольник с верши­нами Найти уравнения его сторон, определить внутренний угол .

Решение. По формуле () находим уравнения сторон:

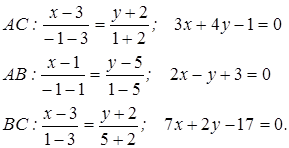
Внутренний угол образован прямыми и AB. Их угловые коэффициенты поэтому

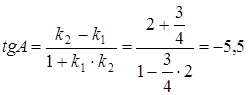
< Предыдущая		Следующая >