61. Теоремы двойственности

Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.

Возможны следующие случаи:

· обе задачи из пары двойственных имеют оптимальные решения;

· одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.

Первая теорема двойственности.

Для двойственных задач линейного программирования имеет место один из взаимоисключающих случаев:

1. В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают: ;

2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.

3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым;

4. Обе из рассматриваемых задач имеют пустые допустимые множества.

Вторая теорема двойственности (теорема о дополняющей нежесткости):

Пусть – допустимое решение прямой задачи, а – допустимое решение двойственной задачи. Для того, чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:

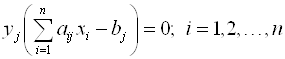
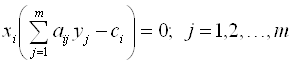
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.

Теорема об оценках:

Значения переменных в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов системы ограничений – неравенств прямой задачи на величину :

.

Диапазон изменения компонент вектора , в котором сохраняется оптимальный базис, называется Областью устойчивости оптимальных оценок.

Экономический смысл первой теоремы двойственности следующий. План производства и набор ресурсов оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции , равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов . Для всех других планов прибыль от продукции всегда меньше или равна стоимости затраченных ресурсов , т. е. ценность выпущенной продукции не превосходит суммарной оценки затраченных ресурсов. Значит, величина характеризует производственные потери в зависимости от рассмотренной производственной программы и выбранных оценок ресурсов.

Контрольные вопросы к лекции 14

1. Понятие математического моделирования.

2. Задача линейного программирования и ее каноническая форма.

3. Целевая функция и система ограничений.

4. Понятие выпуклой линейной комбинации.

5. Базисное, опорное и оптимальное решения.

6. Двойственная задача линейного программирования и объективно обусловленные оценки.

< Предыдущая		Следующая >