55. Лекция 14. Основы линейного программирования

Основные понятия:

Математическое программирование; система ограничений; целевая функция; задача линейного программирования; оптимальное решение; каноническая задача линейного программирования; дополнительная переменная; выпуклое множество; выпуклая линейная комбинация; замкнутое множество; угловая точка; линия уровня; опорная прямая; базисное решение; опорное решение; симплекс-метод; двойственная задача; объективно обусловленные оценки.

Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т. е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т. д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.

Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.

Математическое программирование – это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.

Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т. д.

Построение математической модели экономической задачи включает следующие этапы:

1. Выбор переменных задачи;

2. Составление системы ограничений;

3. Выбор целевой функции.

Переменными задачи называются величины , которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора .

Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т. п.

Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.

Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции:

И соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:

Если целевая функция и система ограничений линейны, то задача математического программирования называется Задачей линейного программирования и в общем виде может быть записана следующим образом:

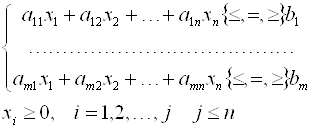
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.

Допустимым решением (планом) задачи линейного программирования называется любой , удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.

Оптимальным решением (Планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.

< Предыдущая		Следующая >