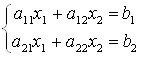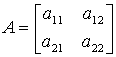51. Правило Крамера решения систем линейных уравнений

Рассмотрим невырожденные системы линейных уравнений, т. е. системы, у которых и определитель матрицы системы отличен от нуля. Определитель матрицы называется определителем системы. Следующая теорема, называемая правилом Крамера, отвечает на второй вопрос.

Пусть дана система двух линейных уравнений с двумя неизвестными:

(13.3)

Коэффициенты этой системы составляют квадратную матрицу второго порядка:

(13.4)

Решим систему (13.3). Для этого умножим первое уравнение системы на , второе – на и вычтем из первого уравнения второе:

.

Аналогично, исключая , получим .

Если , то найдем единственное решение системы: .

Общий знаменатель значений неизвестных и , обозначаемый через , называется определителем матрицы . Это определитель второго порядка. Числителями неизвестных и являются определители тоже второго порядка . Откуда .

Мы получили правило Крамера решения системы двух линейных уравнений с двумя неизвестными.

Правило Крамера. Если определитель системы линейных уравнений с неизвестными отличен от нуля, то система имеет единственное решение: , где
‑ определитель, получаемый из заменой -го столбца столбцом свободных членов.

Невырожденную систему линейных уравнений можно решить и иным способом.

Поскольку матрица ‑ невырожденная, то для нее существует единственная обратная матрица . Умножив обе части уравнения слева на матрицу , получим , откуда .

Мы ответили на три вопроса относительно систем линейных уравнений. Однако применение теоремы Крамера, которая позволила дать этот ответ, приводит к слишком громоздким вычислениям. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса.

< Предыдущая		Следующая >