49. Применение квадратичных форм к исследованию кривых второго прядка

В общем случае кривая второго порядка в базисе 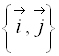описывается уравнением . Ее первые три слагаемые образуют квадратичную форму с матрицей:

.

Задача о приведении кривой к каноническому виду сводится к задаче о приведении к каноническому виду квадратичной формы этой кривой.

Пусть и – собственные значения матрицы , а и 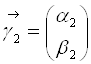– ортонормированные собственные векторы матрицы , соответствующие собственным значениям и .

Ортонормированные векторы и называются главными направлениями этой кривой.

Пусть 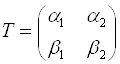является матрицей перехода от ортонормированного базиса 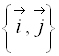к ортонормированному базису .

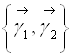Тогда ортогональное преобразование:

Приводит квадратичную форму к каноническому виду , а уравнение кривой – к виду в прямоугольной декартовой системе координат , оси которой направлены вдоль векторов , а начало совпадает с точкой системы координат .

Выделив в этом уравнении полные квадраты, получим , где – некоторые числа. Осуществив параллельный перенос системы координат в новое начало , получим канонический вид уравнения в системе координат . В зависимости от чисел эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.

Контрольные вопросы к лекции №12

1. Понятие квадратичной формы.

2. Построение матрицы квадратичной формы.

3. Канонический и нормальный вид квадратичной формы.

4. Канонический базис квадратичной формы и приведение квадратичной формы к каноническому виду.

5. Канонический базис Якоби.

6. Критерий Сильвестра знакоопределенности квадратичной формы.

< Предыдущая		Следующая >