47. Канонический базис квадратичной формы

Принято считать, что квадратичная форма имеет Канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т. е. при . При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами , т. е.:

.

В этом случае матрица квадратичной формы имеет диагональный вид:

Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

Пусть дана квадратичная форма , Поскольку – симметрическая матрица, для нее существует диагонализирующая ортогональная матрица , такая что:

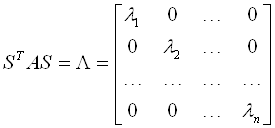
Где – собственные значения матрицы .

Применим к квадратичной форме линейное преобразование , где – матрица-столбец новых переменных ; – матрица, обратная к .

Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Наиболее удобным для исследования является канонический вид, в котором коэффициенты при новых переменных равны +1
или –1, т. е. квадратичная форма имеет вид:

.

Такую запись называют Нормальным видом квадратичной формы. В нем общее число квадратов равно рангу Квадратичной формы.

Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.

Теорема. Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.

Эту теорему называют законом инерции квадратичных форм.

Базис пространства называется Каноническим базисом квадратичной формы , если в этом базисе квадратичная форма имеет канонический вид, т. е. при .

Если – канонический базис , то выражение:

,

Называется Каноническим видом в базисе , где – новый набор неизвестных.

Теорема. Если – разложение вектора по каноническому базису квадратичной формы , то значение на векторе вычисляется по формуле , .

Доказательство:

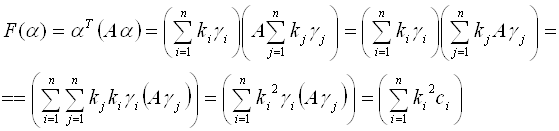
Эта теорема утверждает, что если известны канонический базис Квадратичной формы и ее канонический вид в этом базисе, то для вычисления значения квадратичной формы на векторе достаточно:

1. разложить вектор по каноническому базису :

;

2. коэффициенты разложения подставить вместо неизвестных в канонический вид квадратичной формы:

.

Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется Приведением квадратичной формы к сумме квадратов.

Наиболее часто используются: канонический базис из собственных векторов матрицы и канонический базис Якоби.

Канонический базис из собственных векторов матрицы квадратичной формы

Теорема. Ортонормированный базис пространства , состоящий из собственных векторов симметрической матрицы , , является каноническим базисом квадратичной формы , а выражение – ее каноническим видом в базисе .

Доказательство:

, если , так как – Ортогональная система векторов – канонический базис квадратичной формы .

, так как векторы системы нормированы, то , .

Канонический базис Якоби квадратичной формы

Будем говорить, что матрица удовлетворяет условию Якоби, если определители:

, ,

Называемые Угловыми минорами матрицы , не равны нулю. Очевидно, что , .

Обозначим через матрицу:

.

Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т. д.

Из условия , следует, что и, значит, каждая система уравнений , , где – –й вектор диагональной системы, имеет единственное решение , . Система векторов называется системой векторов Якоби матрицы , которая удовлетворяет условию Якоби.

Теорема. Если матрица квадратичной формы удовлетворяет условию Якоби, то система векторов Якоби матрицы является каноническим базисом квадратичной формы , а выражение:

– ее каноническим видом в базисе .

< Предыдущая		Следующая >