30. Парабола

Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки (фокуса) и данной прямой (директрисы).

Для вывода канонического уравнения параболы ось проводят через фокус перпендикулярно директрисе в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом и точкой пересечения оси с директрисой . Если обозначить через расстояние фокуса от директрисы, то 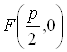и уравнение директрисы будет иметь вид .

В выбранной системе координат уравнение параболы имеет вид:

(7.8)

Это уравнение называется Каноническим уравнением параболы. Из уравнения (7.8) видно, что может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси . Так как уравнение (7.8) содержит только в четной степени, то парабола симметрична относительно оси , и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти .

При неограниченном возрастании неограниченно растет и . Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии.

Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется Вершиной параболы.

< Предыдущая		Следующая >