17. Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении
Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс ![]() , вторая – осью ординат
, вторая – осью ординат ![]() , третья – осью аппликат
, третья – осью аппликат ![]() ; точка
; точка ![]() ‑ начало координат (Рис. 4.4).
‑ начало координат (Рис. 4.4).
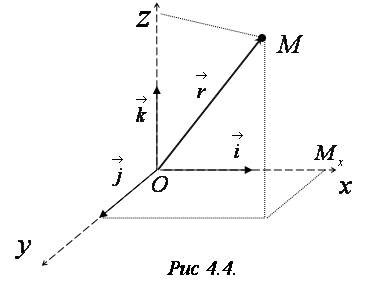
Положение координатных осей можно задать с помощью единичных векторов ![]() , направленных соответственно по осям
, направленных соответственно по осям ![]() . Векторы
. Векторы ![]() называются основными или базисными ортами и определяют базис
называются основными или базисными ортами и определяют базис ![]() в трехмерном пространстве.
в трехмерном пространстве.
Пусть в пространстве дана точка ![]() . Проектируя ее на ось
. Проектируя ее на ось ![]() , получим точку
, получим точку ![]() . Первой координатой
. Первой координатой ![]() или Абсциссой точки
или Абсциссой точки ![]() называется длина вектора
называется длина вектора ![]() , взятая со знаком плюс, если
, взятая со знаком плюс, если ![]() Направлен в ту же сторону, что и вектор
Направлен в ту же сторону, что и вектор ![]() , и со знаком минус ‑ если в противоположную. Аналогично проектируя точку
, и со знаком минус ‑ если в противоположную. Аналогично проектируя точку ![]() на оси
на оси ![]() и
и ![]() , определим ее Ординату
, определим ее Ординату ![]() И Аппликату
И Аппликату ![]() . Тройка чисел
. Тройка чисел ![]() взаимно однозначно соответствует точке
взаимно однозначно соответствует точке ![]() .
.
Система координат называется Правой, если вращение от оси ![]() к оси
к оси ![]() в ближайшую сторону видно с положительного направления оси
в ближайшую сторону видно с положительного направления оси ![]() совершающимися против часовой стрелки, и Левой, если вращение от оси
совершающимися против часовой стрелки, и Левой, если вращение от оси ![]() к оси
к оси ![]() в ближайшую сторону видно совершающимися по часовой стрелке.
в ближайшую сторону видно совершающимися по часовой стрелке.
Вектор ![]() , направленный из начала координат в точку
, направленный из начала координат в точку ![]() называется Радиус-вектором точки
называется Радиус-вектором точки ![]() , т. е.:
, т. е.:
|
|
(4.6) |
Если даны координаты точек ![]() и
и ![]() , то координаты вектора
, то координаты вектора ![]() получаются вычитанием из координат его конца
получаются вычитанием из координат его конца ![]() координат начала
координат начала ![]() :
:![]() или
или ![]() .
.
Следовательно, по формуле (4.5):
|
|
(4.7) |
При сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число все его координаты умножаются на это число.
Длина вектора ![]() равна квадратному корню из суммы квадратов его координат.
равна квадратному корню из суммы квадратов его координат.
|
|
(4.8) |
Длина вектора ![]() , заданного координатами своих концов, т. е. расстояние между точками
, заданного координатами своих концов, т. е. расстояние между точками ![]() и
и ![]() вычисляется по формуле:
вычисляется по формуле:
|
|
(4.9) |
Если ![]() и
и ![]() коллинеарны, то они отличаются друг от друга скалярным множителем. Следовательно, у коллинеарных векторов координаты пропорциональны:
коллинеарны, то они отличаются друг от друга скалярным множителем. Следовательно, у коллинеарных векторов координаты пропорциональны:
|
|
(4.10) |
Пусть точка ![]() делит отрезок между точками
делит отрезок между точками ![]() и
и ![]() в отношении
в отношении ![]() , тогда радиус-вектор точки
, тогда радиус-вектор точки ![]() выражается через радиусы-векторы
выражается через радиусы-векторы ![]() и
и ![]() его концов по формуле:
его концов по формуле: 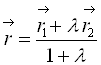 .
.
Отсюда получаются координатные формулы:
 .
.
В частности, если точка ![]() делит отрезок
делит отрезок ![]() пополам, то
пополам, то ![]() и
и 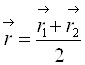 , т. е.
, т. е. 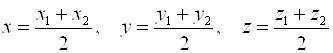 .
.
| < Предыдущая | Следующая > |
|---|
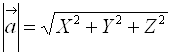 .
.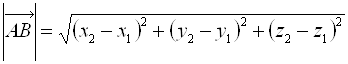 .
.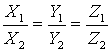 .
.