15. Линейная зависимость векторов

Говорят, что векторы линейно независимы, если из равенства:

(4.3)

Следует, что .

В противном случае векторы называются Линейно зависимыми. Если какой-нибудь вектор можно представить в виде , то говорят, что вектор линейно выражается через векторы .

Теорема. Векторы линейно зависимы тогда и только тогда, когда, по крайней мере, один из них линейно выражается через остальные.

Следствие. Если векторы линейно независимы, то ни один из них нельзя выразить через остальные; в частности, ни один из них не может быть нулевым.

Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой. Любые два неколлинеарных вектора и линейно независимы. В самом деле, предположим, неколлинеарные векторы и линейно зависимы. Тогда, по предыдущей теореме, один из них, например , линейно выражается через второй, т. е. , а это противоречит неколлинеарности и . Следовательно, и - линейно независимы.

Пусть и неколлинеарные векторы, ‑ произвольный вектор компланарный векторам и . Отложим векторы и от одной точки , т. е. построим (Рис.4.3).

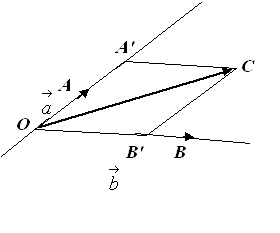
Рис. 4.3.

Из параллелограмма видно, что:

.

Следовательно, любые три компланарных вектора и линейно зависимы.

Любые три некомпланарных вектора и линейно независимы.

Если предположить, что три некомпланарных вектора и линейно зависимы, то один из них, например , линейно выражается через и , т. е. , а это говорит о том, что три вектора и лежат в одной плоскости, что противоречит условию.

Три вектора и линейно зависимы тогда и только тогда, когда определитель, составленный из их координат, равен нулю.

Пусть векторы и в некотором базисе имеют координаты , и соответственно. Тогда векторы и линейно зависимы тогда и только тогда, когда линейно зависимы их координатные столбцы. Значит, векторы и линейно зависимы тогда и только тогда, когда существуют числа , неравные одновременно нулю, что выполняется равенство:

.

Линейная зависимость означает, что существует ненулевой набор коэффициентов такой, что:

(4.4)

Если один из векторов, например, , является нулевым, то система окажется линейно зависимой, т. к. равенство (4.4) будет выполнено при .

Теорема. Векторы линейно зависимы тогда и только тогда, когда один из векторов является линейной комбинацией остальных.

< Предыдущая		Следующая >