08. Соединения. Бином Ньютона

Рассмотрим совокупность различных элементов . Произвольная упорядоченная выборка из этих элементов:

(; )

Называется Соединением. Эта выборка может быть как без повторений, так и с повторениями.

Раздел элементарной математики, в котором для конечных множеств рассматриваются различные соединения элементов, такие, как сочетания, размещения, перестановки, а также все виды соединений с повторениями называется Комбинаторика. Задачи комбинаторики впервые рассматривались в связи с возникновением теории вероятностей, где к задачам комбинаторики приводит подсчет вероятностей на основе гипотезы равновозможных элементарных событий.

Размещениями из элементов по () называют их соединения, каждое из которых содержит ровно различных элементов (выбранных из данных элементов) и которые отличаются либо сами элементами, либо порядком элементов.

Определим число размещений из элементов по .

Будем строить произвольное соединение последовательно. Сначала определим его первый элемент . Очевидно, что из данной совокупности элементов его можно выбрать Различными способами. После выбора первого элемента , для второго элемента остается Способов выбора и т. д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Для Элементов формула приобретает вид:

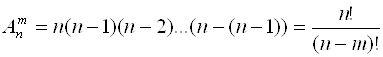
Соединения из элементов, каждое из которых содержит все элементов, и которые отличаются лишь порядком элементов, называются Перестановками .

Перестановки являются частным случаем размещений. Так как каждая перестановка содержит все Элементов множества, то различные перестановки отличаются друг от друга только порядком элементов.

Сочетаниями из элементов по () называют такие их соединения, каждое из которых содержит ровно данных элементов, и которые отличаются хотя бы одним элементом.

Рассмотрим все допустимые сочетания элементов .

Делая в каждом из них Возможных перестановок их элементов, очевидно, получим все размещения из элементов по :

.

Числа являются коэффициентами в формуле бинома Ньютона:

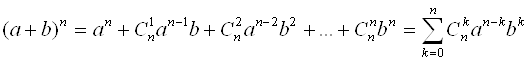
Свойства сочетаний:

1.

2.

3.

4.

5.

Свойства 1 и 2 очевидно следуют из определения , свойства 3 и 4 доказываются с помощью бинома Ньютона, полагая для свойства 3 что и , а для свойства 4 что и . Свойство 5 можно проверить следующим образом:

Это свойство позволяет последовательно вычислять биномиальные коэффициенты с помощью так называемого Треугольника Паскаля:

Здесь каждое число, кроме крайних единиц, является суммой двух вышерасположенных.

< Предыдущая		Следующая >